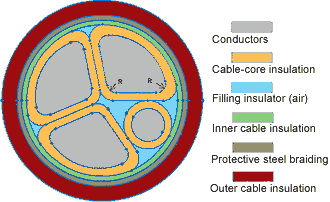
Cable：ActiveField 応用例題

ActiveField技術によって強化されたQuickFieldは、多様な工学分野における物理学の解析のために使用することが可能です。  そして、高度に解析を自動化することができます。そして、QuickField問題の自動生成、解析、ポストプロセシングおよび報告書の生成のために、VBAマクロのセットを伴うマイクロソフトWordドキュメントとしてインプリメントすることができます。より複雑な問題、例えば、ActiveFieldによるケーブル解析のようなテトラ芯ケーブルの解析などに利用可能です。ユーザーが、Visual Basicの知識を持ち、QuickFieldオブジェクト・モデルについて理解しているならば、これらのマクロのソース・コードを分析することが可能です。

このドキュメントは、特定のモデル化パラメータに基づいたケーブルの解析結果を表示します。下記の画像、テーブルおよびグラフは、MS wordのマクロとしてインプリメントされたVBAコードによってコントロールされ、QuickField Professionalバージョンによって自動的に計算されます。また、「対応する問題」はQuickField Studentsバージョンによって解析することもできます。

1. モデルの定義

2. インプット・パラメータ

3. ケーブル・パラメータの計算

4. フィールド・ピクチャー

1. モデルの定義（Model description）

図1  ケーブル・スケッチ

この高電圧用のテトラ芯ケーブルは、３つの三角形と１つの円形コンダクタで構成される断面を形成します。すべてのコンダクタはアルミニウムです。各コンダクタは絶縁され、ケーブル全体として、３層に絶縁されています。ケーブルの絶縁は内部絶縁体と外部絶縁体および絶縁被覆（スチール製テープ）で構成されます。コンダクタの鋭角部はそのフィールド・クラウンを縮小するために面取りされています。コンダクタ間の空気層もまた、空気の絶縁体で満たされています。

一般に、コンダクタの断面積パラメータに従ったケーブルの設計が要求されます。コンダクタの断面積はテーブル１に定義されます。テーブル2〜7は他の入力パラメータについて記述します。

2. インプット・パラメータ（Input parameters）

テーブル  1. コンダクタの幾何学パラメータ

三角形のコンダクタ断面積	120	Mm2
円形のコンダクタ断面積	35	Mm2
スレッド半径（R）	2	Mm

テーブル  2.  絶縁体の幾何学パラメータ

ケーブル芯絶縁の厚さ	2	Mm
内部ケーブル絶縁の厚さ	1	Mm
絶縁スチール被覆の厚さ	1	Mm
外部ケーブル絶縁の厚さ	3	Mm

テーブル  3.  精度

断面積の計算誤差

0.001

Mm2.

テーブル  4. コンダクタの荷重

電流	200	A.
電圧（静電場）	6500	V.
周波数	50	Hz.
電流の位相（静解析用）	0	Deg.

テーブル  5. コンダクタの物理特性

相対誘電率	1
コンダクティビティ（伝導率）	36000000	S/m
熱伝導率	140	W/K·m
ヤング率	6.9e+10	N/m2
ポアソン比	0.33
熱膨張係数	2.33e-5	1/K
密度	2700	Kg/m3

テーブル  6. スチール被覆の物理特性

相対誘電率	1000
コンダクティビティ（伝導率）	6000000	S/m.
熱伝導率	85	W/K·m
ヤング率	2e+11	N/m2
ポアソン比	0.3
熱膨張係数	0.000012	1/K
密度	7870	Kg/m3

テーブル  7.  絶縁体の物理特性

	芯	内部	外部
相対誘電率	1	1	1
コンダクティビティ（伝導率）	0	0	0	S/m
相対電気誘電率	2.5	2.5	2.5
熱伝導率	0.04	0.04	0.04	W/K·m
ヤング率	10000000	10000000	10000000	N/m2
ポアソン比	0.3	0.3	0.3
熱膨張係数	0.0001	0.0001	0.0001	1/K
密度	900	900	1050	Kg/m3

3. ケーブル・パラメータの計算

ケーブルの物理的パラメータは、次のテーブルで示されます。

ケーブルの外部直径はテーブル1と2のコンダクタと絶縁体の幾何学パラメータを使用して計算されます。1メートル当たりケーブルの線形重量は、ケーブル・コンポーネントの幾何学的なパラメータおよび密度から計算されます。全ケーブル密度はすべてのケーブル・コンポーネントを考慮し、計算されます。

テーブル  8.  ケーブル物理的なパラメータ

ケーブルの外部直径	4.28e+01	Mm
重量（メートル当り）	2.74e+00	Kg
ケーブルの密度	1.90e+03	Kg/m2

「コンダクタのキャパシタンス」テーブルは、ケーブル・コンダクタの自己キャパシタンスおよび相互キャパシタンスを保持します。これらの値はチャージ・アプローチを使用し、QuickField静電場問題で計算され、各テーブル行について個別のQuickField問題が解析されます。2つのコンダクタ層のうちの1つは単位チャージを計算し、他方のコンダクタはポテンシャルを推定します。相互キャパシタンスは次式に従います。

C_ij = U_j / Q_i

自己キャパシタンスは同一チャージ・コンダクタでのポテンシャル測定によって計算されます。

テーブル  9.  コンダクタのキャパシタンス、F

	Conductor1	Conductor2	Conductor3	Null-cord
Conductor1	2.53e-10	1.02e-09	1.95e-09	8.43e-10
Conductor2	1.02e-09	2.67e-10	1.02e-09	1.88e-09
Conductor3	1.95e-09	1.02e-09	2.53e-10	8.42e-10
Neutral cord	8.43e-10	1.88e-09	8.42e-10	1.28e-10

コンダクタのインダクタンスは、テーブル10に示します。２〜５列の値は、テーブル4に定義された位相での静磁場問題で計算されます。６〜９列の値は過渡ハーモニック磁場問題で計算されます。すべての値は次式のフラックス・リンケージ・アプローチを使用して得られます。

L_ij = F_j / I_i

テーブルの対角要素は、自己インダクタンス値を表わします。

テーブル  10.  コンダクタのインダクタンス

	静磁場問題				過渡ハーモニック磁場問題
	C-1	C-2	C-3	0-cord	C-1	C-2	C-3	0-cord
Conductor1	1.15e-05	1.12e-05	1.11e-05	1.13e-05	6.17e-06	5.99e-06	5.94e-06	6.02e-06
Conductor2	1.12e-05	1.15e-05	1.12e-05	1.11e-05	5.99e-06	6.17e-06	5.99e-06	5.93e-06
Conductor3	1.11e-05	1.12e-05	1.15e-05	1.13e-05	5.94e-06	5.99e-06	6.17e-06	6.02e-06
Neutral cord	3.89e-10	3.84e-10	3.89e-10	4.04e-10	6.02e-06	5.93e-06	6.02e-06	6.27e-06

テーブル11は、インピーダンスおよびインピーダンス等価値を含んでいます。静電場問題では、コンダクタの1メートル当たりのインピーダンス（等価抵抗）は次式によって計算されます。

R = l / (r·S)

静電場問題の1メートル当たりジュール熱は、次式によって計算されます。

P = I_A² · R

ここで、I_A は平方2乗平均電流を示し、R はコンダクタ・インピーダンスを示します。

過渡ハーモニック問題におけるコンダクタのインピーダンスは、コンダクタの比（平均ポテンシャル／総電流密度）の複素数値としてオームの法則から計算されます。この比率の実数部分は抵抗を表し、虚数部はリアクタンスを表し、振幅係数はインピーダンスを表します。過渡ハーモニック磁場問題のジュール熱は対応するQuickField積分関数を使用して計算されます。

テーブル  11. コンダクタのインピーダンス

	静電場問題		過渡ハーモニック磁場問題
	Conductors	Null cord	Conductor1	Conductor2	Conductor3
Impedance, W	2.31e-04	7.94e-04	2.40e-04	2.55e-04	2.80e-04
Resistance, W	2.31e-04	7.94e-04	2.15e-04	2.37e-04	2.59e-04
Reactance, W	0.00e+00	0.00e+00	1.08e-04	9.41e-05	1.06e-04
Joule heat, W	4.63e+00	0.00e+00	4.71e+00	4.74e+00	4.71e+00

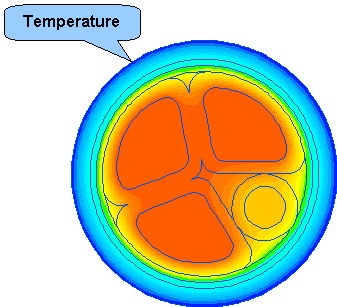
生成された温度場は、伝熱問題の過渡ハーモニック問題からエクスポートされます。QuickFieldのシミュレーション結果、ケーブル外表面平均温度、ケーブル表面からの熱フローおよびすべてのコンダクタの平均温度を観察することができます。平均温度は示された相対値であり、周囲温度は摂氏20℃であると仮定しました。

テーブル  12. ケーブル熱パラメータ

外部表面の平均温度			2.35e+01		°C
熱フロー			1.42e+01		W
コンダクタ平均温度、℃
Conductor1	Conductor2	Conductor3		Null-cord
4.59e+01	4.68e+01	4.59e+01		3.93e+01

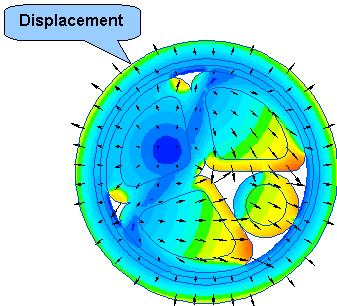
応力解析問題は、連成問題であり、それは熱伝導問題からの温度場および過渡ハーモニック磁気問題からの磁力をインポートします。この磁場や熱の荷重により、ケーブル・コンポーネントは変形されます。それらの変形数値は次のテーブルで示されます。

テーブル  13.  応力解析問題の結果

最大変位	5.14e-02	Mm
最大応力値（Mohr criteria value）	8.16e+07	N/m2

強度値はケーブル強度解析にとって重要です。

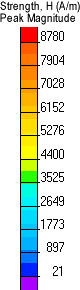
テーブル  14. 強度

最大ピークの強度値

8.78e+03

A/m

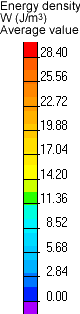
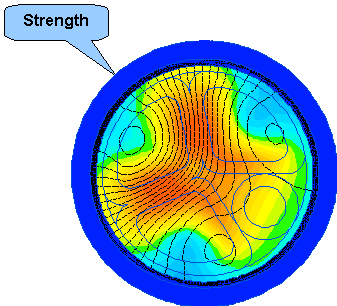
「強度」フィールドおよび「総電流密度」、「エネルギー密度」、「瞬時フラックス密度」、「温度」および「変位」のフィールド画像を以下に示します。

４. フィールド・ピクチャー（Field pictures）

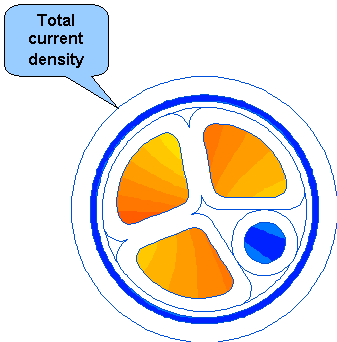
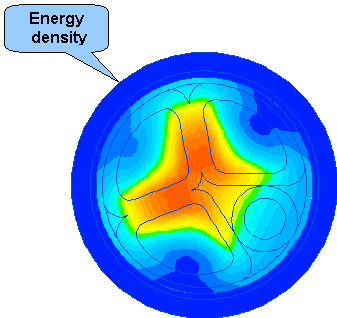
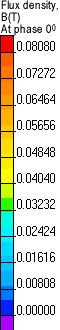
●掲載例題については細心の注意を払っていますが、予告なしに内容の見直しおよび変更をさせていただくことがあります。本サイトを閲覧、ダウンロード、リンク、転載、その他の行為は著作権者の規程に同意したものとします。これによって生じる利用者各位のいかなる障害についても、責任を負うものではないこととします。あらかじめ、ご了承ください。