|
モード解析の基本として、単純な質量-バネ-減衰のSDOF系さらにMDOF系に関して、モードデータがどのように計算されるかを説明します。また、STARSystemのカーブフィット処理による構造物の振動特性を求める方法および構造変更や外力応答のシミュレーションについて解説します。
1.振動モデル
振動学では、まず1自由度振動系についての議論から始め、それを多自由度振動系に展開するのが一般的です。それぞれの振動モデルは、「質量(M)」と「ばね(K)」と「ダンパ(C)」を用いて、一般に図1のように表現されます。
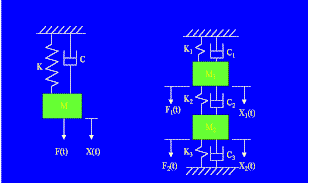
図1 1自由度系(左)と多自由度系(右)の振動モデル
2.運動方程式
まず、次式で表される運動方程式について、考えてみましょう。
[M]{X”(t)} +
[C]{X’(t)} + [K]{X(t)} =
{F(t)}
(1)
この式の左辺の3項は、左から順に、「慣性力」、「減衰力」、「弾性復元力」を表しており、それらを合計したものが「内力」に相当します。一方、この式の右辺は「外力」を表しています。すなわち、運動方程式は内力と外力が釣り合った状態を示しています。多自由振動系の場合は、左辺の3項の係数がマトリックスの形になり、系が n自由度なら、[M], [C], [K]のいずれもn行n列の正方マトリックスになります。
3.運動方程式の非連成化と正規モード法
前述の多自由度振動系の運動方程式は、次式のように、n自由度の連立微分方程式を表しています。
(m11x1” + m12x2” + … +
m1nxn”) + (c11x1’ + … + c1nxn’) + (k11x1 + … + k1nxn) =
f1
(m21x1” +
m22x2” + … + m2nxn”) + (c21x1’ + … + c2nxn’) + (k21x1
+ … + k2nxn) = f2
……………………………
(mn1x1” + mn2x2” + … +
mnnxn”) + (cn1x1’ + … + cnnxn’) + (kn1x1
+ … + knnxn) = fn (2)
これを直接解くことは、通常は少し厄介な仕事です。そこで「正規モード法」では、固有モードの直交性を利用して、多自由度振動系の運動方程式を非連成化します。これは、数学的にはマトリックスの対角化を意味します。したがって、上に示したn自由度の連立微分方程式は、次に示すように、固有モードごとに互いに独立な1自由度微分方程式に分解されます。
m11x1” + c11x1’ + k11x1 =
f1
m22x2” + c22x2’ + k22x2 =
f2
…………
mmmxm”+cmmxm’+kmmxm
= fm (3)
…………
mnnxn” + cnnxn’ + knnxn =
fn
このようにすれば、複数の1自由度微分方程式を互いに独立に解くことによって、多自由度の連立微分方程式を解く場合と同等の解を得ることができます。しかも、一般に不必要な高次の固有モードを省略でき、解くべき1自由度微分方程式の数を大幅に減じて計算時間の短縮を図ることができます。
正規モード法は、多自由度振動系の運動方程式を非連成化することを狙いとした手法です。この手法では、まず変換マトリックス[U]を導入して、
{X(t)}=[U]{z(t)} (4)
とおき、これを前述の運動方程式に代入します。ここで、{X(t)}は物理的な変位ベクトル、{z(t)}はモード変位ベクトルを表します。n行m列のこの変換マトリックス[U]は、モードシェープ・マトリックスとも呼ばれます。
さて、(4)式を前述の運動方程式に代入すると、次式のように書きかえられます。
[m]{z”(t)} + [c]{z’(t)} + [k]{z(t)} = [U]t{F(t)} (5)
ここで、mはモード数を表します。[m], [c], [k]は、それぞれ「モード質量マトリックス」、「モード減衰マトリックス」、「モード剛性マトリックス」と呼ばれ、次式で表されるように、いずれもm行m列の対角マトリックスです。
[m] = [U]t[M][U]
[c] =
[U]t[C][U] (6)
[k] = [U]t[K][U]
前述のモードマトリックスを使って書きかえられた運動方程式は、モード質量がすべて1(単位)になるようにモードベクトルをスケーリングすることによって、次のように、さらに便利な形に変換できます。
[I]{z”(t)} + [2ζΩ]{z’(t)} + [Ω2]{z(t)} = [U]t{F(t)} (7)
ただし、[I] = [U]t[M][U] (単位モード質量マトリックス)
[2ζΩ] =
[U]t[C][U] (モード減衰マトリックス)
[Ω2] = [U]t[K][U] (モード剛性マトリックス)
この式は、実験モード解析において最終的に求めようとしている、構造物の動特性(モード特性)を含んだ形で表されています。
さて、構造物の動特性を求める方法には、基本的に2つの方法、すなわち、
●有限要素法に基づいてモデル化を行い、同次方程式の解として構造物の動特性を求める方法。(これは固有値解析とも見なすことができ、固有値からモード周波数とモード減衰が得られ、固有ベクトルからモードシェープが得られる。)
●実験データから構造物の動特性を求める方法。(この方法では、周波数領域の構造物のモデルと実際の計測によって構造物からから得られる周波数応答関数(FRF)データが用いられる。周波数応答関数の計測は、FFTスペクトラム・アナライザで行う。)
があります。ここで述べる実験モード解析法は、もちろん後者の方法です。
4.ラプラス変換
これまで述べてきた運動方程式は、時間領域の微分方程式で表されています。ラプラス変換は、この時間領域の微分方程式を、それと等価な周波数領域の代数方程式に変換する数学的手法です。そこで、(1)式の運動方程式をラプラス変換すると、
[[M]s2 + [C]s + [K]] {X(s)} = [B(s)]{X(s)} = {F(s)} (8)
となります。この式の左辺の[ ]でくくられたラプラス変数sに関する2次式は、「システム・マトリックス」と呼 ばれ、これを[B(s)]で表すと、
[B(s)] = [M]s2 + [C]s + [K] (9)
となります。(8)式の解は、固有値がシステム・マトリックスの行列式を、|B(s)|=0としたときの、ラプラス変数 s の値となるような固有値問題を表しています。
5.伝達マトリックス
伝達マトリックスは[H(s)]は、前述のシステムマトリックスの逆マトリックスとして定義されます。 したがって、(8)式で表されるラプラス変換された運動方程式は、次のような別の表現に置き換えることができる。
{X(s)} = [H(s)]{F(s)} (10)
次式で示したn行n列の伝達マトリックスの各要素は、ラプラス変数の関数で、伝達関数と呼ばれています。個々の伝達関数は、ある特定の入力加振自由度とある特定の応答自由度との間の、構造物の動特性を完全に記述したものであり、したがって伝達マトリックスは完全なダイナミックモデルを表したものです。
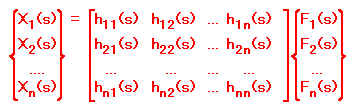 (11) (11)
システムマトリックス[B(s)]の要素はラプラス変数sの2次関数であり、伝達マトリックス[H(s)]はそのシステムマトリックスの逆マトリックスとして定義されますから、[H(s)]の要素は各伝達関数の分母において[B(s)] の行列式を持つ多項式の関数になります。振動モデルがn次元であれば、[B(s)]は2次の多項式
(これを特性方程式という)となり、2n個の根かn対の複素共役根(複素固有値または極という)を持ちます。行列式|B(s)|の根がすべて相異なると仮定すると、[H(s)]は次のような部分分数の形で書き表すことができます。
 (12) (12)
部分分数の各項は、分母に極の値が入っており、分子にはレジデュと呼ばれる定数が入っています。[Rk] は、k番目の極に対するレジデュマトリックスと呼ばれるn行n列の正方マトリックスです。上式から明らかなように、s=pk
または s=pk' のとき伝達関数は無限大となります。そしてそのときの周波数がいわゆる固有振動数であり、モード特性としてのモード周波数(共振周波数)に対応します。
伝達マトリックスを(12)式のような部分分数表現で書き表した後、分子のレジデュマトリックスをモードベクトル(モードシェープ)の項で書き直すと、(13)式に示すように、伝達マトリックスはさらに簡単なものになります。ただし、ukはk番目のモードベクトルです。
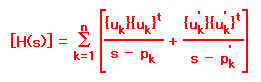 (13) (13)
これは、伝達マトリックス(すなわち、完全なダイナミックモデル)が、モードパラメータを含むパラメトリックな表現に置き換えられたことを意味します。しかもこれは、(7)式で表されたダイナミックモデルと完全に等価です。このことから、「実験において実際に測定された伝達マトリックスと等価な伝達マトリックスを、計算によって組み立てることさえできれば、モードパラメータを求めることができる」ということが分かります。
6.実験モード解析法
以上のことから、実験モード解析では、対象構造物をn行n列の伝達マトリックスを使ってモデル化し、実際の加振試験を通してそのマトリックスの1行分、もしくは1列分に相当するn個の伝達関数を測定(残りは計算によって補完)します。そして、カーブフィッティング(曲線適合)と呼ばれる手法を用いて、測定した伝達関数と等価な伝達関数を計算によって組み立て、対象構造物のモード特性(モード周波数(共振周波数)、モード減衰比、モードシェープ)を求めます。これらのモード特性は、「モードパラメータ」と呼ばれています。
6.1 実験モード解析の標準的手順
実験モード解析の標準的な手順を示すと、以下のようになります。
①初期設定
②構造物の形状定義
③周波数応答関数の計測
④モードの識別/カーブフィッティング/モードパラメータの推定
⑤結果の評価(モードアニメーションなど)
⑥結果の応用(構造変更シミュレーション、外力応答シミュレーション、実稼動解析、システム同定など)
このうち、⑤と⑥は実験モード解析そのものではなく、いわばポスト・プロセッシング(後処理)に属するものです。④が実験モード解析における最も重要なプロセスであること、すなわちその要となるカーブ・フィッティングの精度が最も重要であることは、いうまでもありません。
6.2 周波数応答関数の定義と計測方法
もう一度、(10)式を見てみましょう。これは伝達マトリックスを使って表した運動方程式ですが、入力加振{F(s)}と出力応答{X(s)}の関係を表す式と考えることもできます。これは、伝達マトリックスの要素である伝達関数についても同様です。すなわち、伝達関数は系における入力と出力の比として定義されます。振動学の分野では、これらの入力も出力も振動数(周波数)で表されるものが多いことから、振動数(周波数)を独立変数に見たてて、その関数として定義した伝達関数のことを、特に周波数応答関数(FRF)と呼んでいます。したがって、実験モード解析法でも、正しくは伝達関数のことを周波数応答関数といいます。
周波数応答関数(FRF)マトリックスの要素を求める最も簡単な方法は、一度に一つずつ周波数応答関数を測定することです。図2に示した簡単な2次元の場合は、FRFマトリックスの左上の要素h11(ω)は、点番号1で構造物を加振し、点番号1でその応答を測定することによって計測されます。そして、FRF は応答のフーリエ変換を加振のフーリエ変換で除して表現されます。同様に、第1行の2番目の要素
h12(ω)は、点番号2で構造物を加振し、点番号1での応答のフーリエ変換を点番号2での加振外力のフーリエ変換で除すことによって計測されます。2行目の要素についても、同様な方法で計測されます。
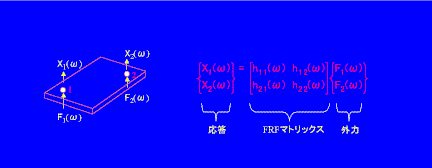
図2 周波数応答関数の測定方法
6.3 カーブフィッティングによるモードパラメータの推定
通常の加振試験において得られる振動モードは一般に連成していますので、その連成の度合い(隣接するモード共振曲線による影響の度合い)によって、適用するカーブフィッティングの手法を選択しなければなりません。カーブフィッティングの手法は、これまでに数多く考案されてきましたが、それらは
①1自由度法(SDOF法)
②多自由度法(MDOF法)
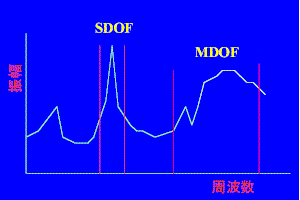
図3 SDOF法とMDOF法の適用選択に大別されます。図3は、モード連成の度合いに応じて適用するカーブフィッティング手法の違いを示したもので、図のように、連成の度合いいが弱い場合はSDOF法を、また連成の度合いが強い場合はMDOF 法を、それぞれ適用します。
1自由度法のカーブフィッティング手法の一つで、よく知られた「多項式法(ポリノミアル法)」は、各振動モードに対して、モード周波数、モード減衰比、モードレジデュを同時に推定できる多項式型のカーブフィッティング・アルゴリズムです。この手法では、周波数応答関数(FRF)を次式のように定義します。
H(jω) = (Rk2σk + R1kωk +
jR2kω)/(σk2 + ωk2ω + 2jσkω)+ A0 + A1(jω) + A2(ω2) (14)
この手法では、カーブ・フィッティングの結果、モード周波数(ωk)、モード減衰率(σk)および複素レジデュ(Rk=R1k+R2k)が得られます。また、測定データの帯域において帯域外モードの影響に対する補正を行う3つの補正項の係数(A0, A1, A2)も、カーブ・フィッティングの過程で求められます。
7.モード解析ソフトウェア
市販されているパソコン用の実験モード解析ソフトウェアの中で、もっとも多くのテスト・エンジニアに活用されているSTAR Systemについて、簡単に触れておきましょう。(詳しくは、このホームページの「システム情報」をご覧になるか、下記の電子メールアドレスに関連資料をご請求下さい)。
|