IMPULSE TECHNIQUE FOR STRUCTURAL FREQUENCY RESPONSE TESTING

By William G. Halvorsen, Anatrol Corporation and David L. Brown, University of Cincinnati

Structural frequency response testing, also known as "modal analysis," is becoming an integral part of the development and testing of a wide range of industrial and consumer products. It is an essential tool for the definition and solution of many types of structural dynamics problems, such as fatigue, vibration, and noise. This article discusses one of the most useful techniques for experimental structural frequency response testing-one based upon excitation of the structure with an impulsive force. In many situations, this is the simplest and fastest of the various techniques commonly used today. However, the nature of the excitation and response signals in the impulse technique requires special signal processing techniques if accurate frequency response measurements are to be obtained. This article discusses the application of the impulse technique and reviews the special problems encountered in practice and the techniques that have been developed for dealing with those problems.

Knowledge of the dynamic characteristics of structural elements often means the difference between success and failure in the solution of complex noise and vibration problems. The effects of structural resonances-conditions of relatively low dynamic stiffness-can lead to seriously reduced effectiveness of isolation elements and result in significantly increased dynamic response of sound radiating or vibration exposure elements. Quantitative knowledge of the frequencies, damping, and mode shapes associated with structural resonances aids in understanding how forces are generated and transmitted throughout mechanical systems and allows intelligent evaluation of various noise and vibration control modifications and treatments. The determination of the resonance characteristics of structures is termed "modal analysis." The purpose of this paper is to review in detail one particularly useful technique for experimental modal analysis, a technique employing the application of an impulsive force to the structure.

In two previous papers, the theory of modal analysis was reviewed and a number of techniques for experimental modal analysis were discussed, including swept­sine excitation, pure­random excitation, pseudo­random excitation, periodic­random excitation, and various forms of transient excitation.12 The impulse technique falls into the class of transient excitation. It deserves particular attention because, for a wide range of structures, it is the simplest and fastest technique for obtaining good estimates of the required frequency response information. There are, however, a number of errors that can occur in the application of the impulse technique and there are certain types of struc­ for which the impulse technique is ill­suited. The major errors encountered in the application of the impulse technique will be discussed along with the signal processing and experimental techniques applicable to impulse testing.

Theory

Frequency Response Function. The measurement of the frequency response function is the heart of modal analysis. The frequency response function H(f) is defined in terms of the single input/single output system, shown in Figure 1, as the ratio of the Fourier transforms of the system output or response v(t) to the system input or excitation u(t), Equation 1

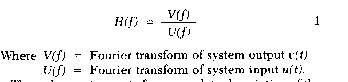
Where V(f) = Fourier transform of system output v(t)
U(f) = Fourier transform of system input u(t).

The only requirements for a complete description of the frequency response function are that the input and output signals be Fourier transformable, a condition that is met by all physically realizable systems, and that the input signal be non­zero at all frequencies of interest. If the system is nonlinear or time­variant, the frequency response function will not be unique, but will be a function of the amplitude of the input signal in the case of a nonlinear system and a function of time in the case of a system with time­varying properties.

The frequency response function may be computed directly from the definition as the ratio of the Fourier transforms of the output and input signals. However, better results are obtained in practice by computing the frequency response function as the ratio of the cross­spectmm be­ the input and output to the power spectrum of the input, Equation 2. This relationship is derived by multiplying the numerator and denominator of the right­hand side of Equation 1 by the complex conjugate of the input Fourier transform.

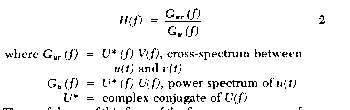
The usefulness of this form of the frequency response function can be seen by considering the practical single input / single output measurement situation illustrated in Figure 2, where m(t) and n(t) represent noise at the input and output measurement points respectively.

The measured frequency response function H^'(f) is given by the expression:

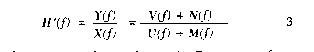
where the upper case letters denote the Fourier transform of the corresponding time domain signals.

In this form, the measured frequency response will be a good approximation of the true frequency response only if the measurement noise at both the input and output measurement points is small relative to the input and output signals. Multiplying the numerator and denominator of the right­hand side of Equation 3 by the complex conjugate of X(f) yields

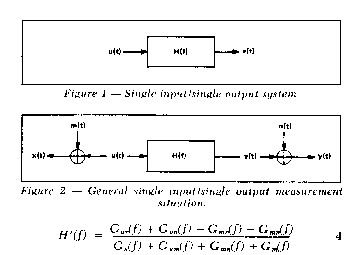
Now, if the measurement signals signals and and are noncoherent with each other and with the input signal u(t), then the expected value of the cross­spectrum terms involving m and n in Equation 4 will equal zero, yielding

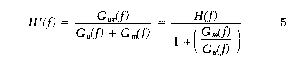
where H(f)is the desired true frequency response function.

Thus, if the noise­to­signal ratio at the input measurement point [G_m(f)/ G_uf)] is much less than 1, the measured frequency response will closely approximate the desired true frequency response function.

It should be pointed out here that there is an inherent bias error associated with the computation of the cross-spectrum and the magnitude of this bias error is inversely proportional to the number of averages in the computation. Thus, the greater the measurement noise, the greater the number of averages required to approach the expected value of the cross­spectrum between the input and the output measurement signals. With measurement technigues employing many averages, the bias error can usually be reduced to an insignificant level so that it is only necessary to minimize the noise in the measurement of the input signal. However, if there is significant measurement noise and only a few averages are used, then the computed values of the cross­spectrum terms involving the noise signals in Equation 4 can be large relative to the true cross-spectrum, with resulting large errors in the measured frequency response function. In general, only a few averages are used in the impulse technique; otherwise, one of its major advantages - its speed - is lost. Therefore, it is important to minimize measurement noise in both the input and output signals when using the impulse technique. The cross­spectrum bias error and its effects are discussed in more detail in Reference 3.

Coherence Function. There is another important reason for computing the frequency response function in terms of the cross­spectrum: it allows the computation of the coherence function between the input anti output signals. The coherence function is defined by the equation

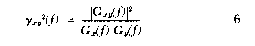
According to the definitions of the power spectrum and the cross­spectrum, the coherence function will he identically equal to 1 if there is no measurement noise and the system is linear. The minimum value of the coherence function, which occurs when the two signals are totally uncorrelated, is 0. Thus, the coherence function is a measure of the contamination of the two signals in terms of noise and nonlinear effects, with very low contamination indicated for values close to 1.

Since the cross­spectrum is included in the definition of the coherence function, the cross­spectrum bias error must be reduced to an acceptable level if a good statistical estimate of the coherence function is to be achieved. As stated above, the number of averages used in the impulse technique is usually not great enough to significantly reduce the bias error. However, the coherence function is still useful for indicating the importance of noise in the impulse technique. This is because noise in the signals causes variance in the value of the coherence function with frequency. This effect is illustrated in the section on measurement procedures.

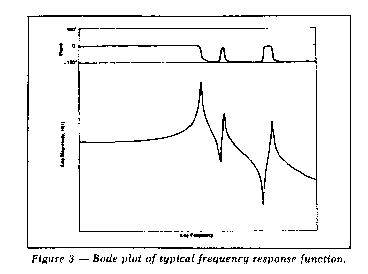
Display of Frequency Response. The frequency response function is complex - that is, it has associated with it both magnitude and phase. Therefore, it can be displayed in a number of forms, including magnitude and phase versus frequency, real and imaginary magnitudes versus frequency, and imaginary magnitude versus real magnitude. Each of these types of displays has its own particular usefulness. The most common type of display for structural frequency response data is magnitude and phase versus frequency, with the magnitude and frequency plotted logarithmically. This type of display, with the magnitude in terms of compliance (ratio of displacement to force), is called a Bode plot. In this form of the frequency response function, resonances occur as peaks in compliance plots (points of maximum dynamic weakness) and all resonance peaks of equal damping have the same width regardless of resonance frequency. Lines of constant dynamic stiffness have zero slope, and mass­dominated frequency response lines have a ­12 dB­per­octave slope. Figure 3 shows an example of a Bode plot of a measured frequency response function.

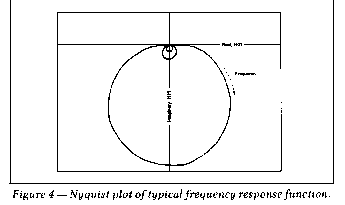
Resonances occur as nearly circular arcs in the complex plane (real versus imaginary plot) with frequency increasing in a clockwise direction around the arc. In the case of real normal modes (which occur in systems with relatively low damping and with resonances well­separated in frequency), each resonance arc is approximately tangent with and lies below, the real axis and is symmetric about the imaginary axis when the frequency response is expressed as compliance. The complex plane plot is useful when certain types of analytical curve fitting operations are being performed on the frequency response data. Figure 4 shows the complex plane plot of the frequency response function shown in Figure 3.

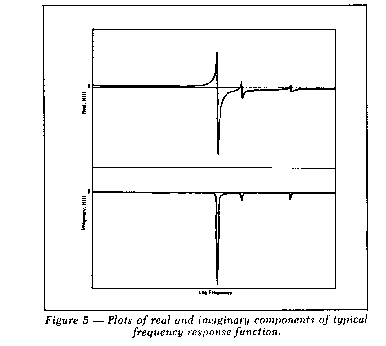
The plots of the real and imaginary magnitudes of frequency response versus frequency are most useful when dealing with real normal modes. In this case the resonances will occur as peaks in the imaginary magnitude plot and the real magnitude will pass through zero at the resonance frequency when the frequency response is expressed as compliance. Figure 5 shows the real and imaginary plots for the data in Figure 3.

The frequency response characteristics of a structural element are determined by measuring a set of cross-frequency response functions as discussed in Reference 1. The cross­frequency response functions may be obtained by exciting at one location on the structure and measuring response at various locations, or by measuring the response

at a single location to excitation at various locations. The resulting frequency response functions comprise one column of the transfer matrix in the first case, and one row of the transfer matrix in the second case. Either set will, in general, completely define the modal characteristics ofthe structural element. In mathematical terms the set of frequency response functions yields the eigenvalues and eigenvectors, which are, in general, complex terms. The real part of an eigenvalue is the damping and the imaginary part is the frequency associated with a given resonance. Each eigenvector defines a resonance mode shape.

With real normal modes, each point on a structure is either exactly in­phase or exactly 180 degrees out­of­phase with any other point at the resonance frequency. Certain types of damping which are often encountered in practice will cause the eigenvectors to have non­zero imaginary components, resulting in complex mode shapes. When a mode is complex, the relative phase associated with a point on a structure is some value other than O or 180 degrees, with the result that node lines (lines of zero deflection) are not stationary. Precise description of complex modes requires that some type of analytical curve fitting technique be applied to the frequency response data.

Measurement of Frequency Response. The frequency response function of an operating system can be computed if the system input and output signals meet previously stated requirements of Fourier transformability and non-zero value, assuming the system input and response can be measured. However, in practice there are usually multiple inputs to the system - either several inputs at different locations or inputs in more than one direction at a given location. In the case of multiple coherent inputs, the complexity of the analysis is greatly increased. For this reason, and the difficulty of accurately monitoring operating inputs, frequency response measurements are usually made by applying the system input "artificially" through some type of exciter. It is in the form of the input signal and the way it is applied to the structure that the wide variety of frequency response testing techniques arises.

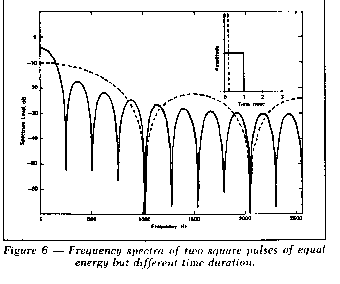
The usefulness of the impulse technique lies in the fact that the energy in an impulse is distributed continuously in the frequency domain rather than occurring at discrete spectral lines as in the case of periodic signals. Thus, an impulse force will excite all resonances within its useful frequency range. The extent of the useful frequency range of an impulse is a function of the shape of the impulse and its time duration. Figure 6 shows the frequency spectra of two square pulses of equal energy but different duration. For a square pulse the frequencies of the zero crossings are at integral multiples of the inverse of the time duration of the impulse, illustrating the very important inverse relationship between the time duration of an impulse and its frequency content.

The useful frequency range of an impulse is also a function of the shape of the impulse. Figure 7 shows three

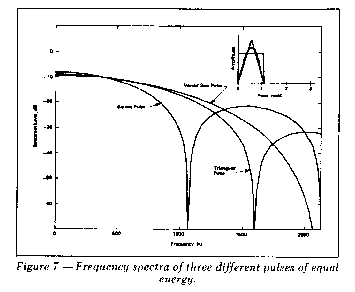
different pulses of equal energy and time duration and their corresponding frequency spectra. By varying the weight and hardness of an impacting device and the manner in which the impact is applied, the shape and time duration of the impulse produced can be varied to suit the measurement requirements. Such practical will be further discussed in the section on experimental measurement techniques.

Nonlinearities in Structures

Excitation of a nonlinear system by a pure­random signal will yield the best estimate (in a mean­square sense) of the linear system response. Excitation by a pure sine wave is also useful for studying nonlinear systems because it allows precise control ofthe input spectrum level. However, the impulse technique, because of its very high ratio of peak level to total energy, is particularly ill­suited for testing nonlinear systems. Therefore, it is important to understand the various types of nonlinearities that can occur in structural systems and to be able to recognize nonlinearities in measured frequency response functions.

One of the most common types of nonlinearities encountered in structures is that due to clearance between parts. This type of nonlinearity is frequently encountered, for example, when testing gear systems and shafts mounted in bearings. The effects of this type of nonlinearity on measured frequency response functions when using impulse excitation are poor estimates of static stiffness values and poor repeatability of the frequency response estimates. Also, the apparent damping in the estimates will be greater than the actual examples.

The best method of dealing with this type of nonlinearity is to preload the system to take up clearances. Care must be taken when this is done, however, because any preload will change the boundary conditions of the structure and can itself lead to erroneous frequency response estimates. The usual approach is to apply the preload through a very soft spring so that the resonances associated with the preload lie below the frequency range of interest.

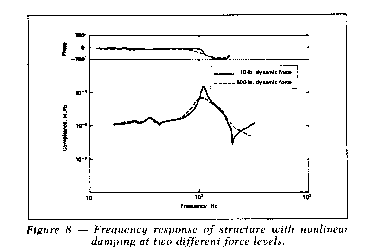
Another type of nonlinearity that is frequently encountered is nonlinear damping. Nonlinear damping effects are usually associated with joints in the structure, where the damping is a function of the relative displacement at the joint. In general, the frequency response estimates obtained by the impulse technique will agree most closely with those obtained with a low level of continuous excitation. However, if the point of excitation is close to a location where nonlinear damping occurs, there will be high relative motion at that location, and the apparent damping in the measured frequency response will be high. In systems with low damping, this will give the measured frequency response a discontinuous appearance, due to the varying level of damping as the response to the impulse attenuates with time. This type of nonlinearity is illustrated in Figure 8, which shows frequency response measurements on a machine tool with different force excitation levels. The frequency response measurements were made with swept­sine excitation.

The third type of nonlinearity that commonly occurs in structures is load­sensitive stiffness, where the spring rate of elastic elements either increases or decreases with load. The most direct way to identify this type of nonlinearity is to measure frequency response as a function of static preload and observe the change in resonance frequencies. This type of nonlinearity is illustrated in Figure 9, which shows frequency response measurements on a pump with three different levels of preload.

Signal Processing

The particular characteristics of an impulsive force signal and the resulting structural response signal make the impulse technique especially susceptible to two problems: noise and truncation errors. While these problems occur to some extent with other frequency response testing techniques, their unique importance in the impulse technique requires special signal processing methods.

Force Signal. It was pointed out in the previous section that the usable frequency range for an impulse depends on the shape and time duration of the impulse. In order to insure that there is sufficient force over the frequency range of interest, it is necessary that the first zero crossing of the Fourier transform of the impulse be well above the maximum frequency of interest. For a given time duration the first zero crossing occurs at the lowest frequency for a square pulse. For that type of pulse the first zero crossing occurs at a frequency equal to the inverse of the time duration. A good rule of thumb, then, is to insure that the duration of the impulse is less than 2(delta)t, where (delta)t is the sampling interval in the analog­to­digital conversion process. This would put the first zero crossing of the Fourier transform of a square pulse at the Nyquist folding frequency, and the first zero crossing of other pulse shapes above the Nyquist folding frequency.

The sample length is equal to N(delta)t where N is the number of digital values in each sample. A typical value of N is 1024. Thus, the duration of the impulse is very short relative to the sample length. This means that the total energy of noise represented in the time­sample can be on the order of the energy of the impulse, even for high signal­to­noise ratios. The noise problem is further aggravated when employing the zoom transform, which yields increased resolution in a given frequency band by effectively increasing the sample length.

With other techniques, the effects of noise are reduced by averaging the power spectrum and cross­spectrum functions prior to the computation of the frequency response function. However, only a few averages are usually used in the impulse technique. Otherwise, the time advantage of the technique is lost. Therefore, special time­sample windows have been developed for the impulse technique.

At first thought it might seem appropriate to just set all time­sample values beyond the impulse to zero, since it is

known that the true signal value after the impulse is zero. However, this would be equivalent to multiplying the signal by a narrow rectangular window. In applying any type of window, it is important to keep in mind that multiplication; by a window in one domain is equivalent to convolution of the Fourier transforms of the window and the data in the other domain, resulting in distortion of the transformed signal. This distortion will be minimized by minimizing the width of the main lobe of the window transform and suppressing its side lobes. However, there is a fundamental conflict between these requirements and the reduction of noise in the time­sample because both the width of the main lobe and the amount of noise reduction are inversely proportional to the width of the window in the time domain. To further complicate the situation, suppression of the side lobes is generally achieved at the expense of broadening the main lobe.

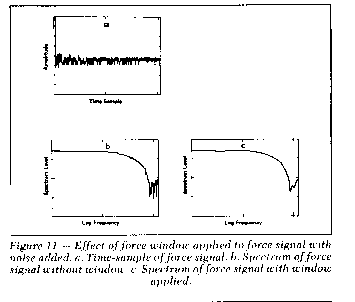
A good compromise has been arrived at in practice the form of a window with unity amplitude for the duration of the impulse and a cosine taper, with a duration of 1/16 of the sample time, from unity to zero. This window is shown in Figure 10. Figure 11 shows the results of applying the force window to an impulse signal with significant measurement noise. Comparison of the computed frequency response functions with and without the window applied shows that the window substantially improves the frequency response estimate.

Response Signal. Noise problems may also be encountered in the response signal, particularly when dealing with heavily damped systems and when using zoom transform analysis. In both cases the duration of tile response signal may be short relative to the total sample time, so that noise may comprise a significant portion ofthe total energy in the time­sample even with relatively high signal­to­noise ratios. Another error in the response signal that is encountered when testing lightly damped structures occurs when the response signal does not significantly decay in the sample window. In this case the resulting timesample is equivalent to multiplying the true response signal by a rectangular window, with the result that the frequency resolution may not be sufficient to resolve individual resonances.

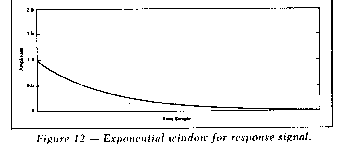
An exponential window has been developed to reduce the errors that occur in both situations described above. The window shape is shown in Figure 12. The window decays exponentially from 1 to a value of 0.05 in the sample time. It can be applied directly to the time­sample of the response signal or to the impulse response function. As with all windows, the exponential window does change the resulting measured frequency response function; but its only effect is to increase the apparent damping in the resonances. It does not change the resonance frequencies and, because the effect of the exponential window is the same on all frequency response measurements, it will not alter the measured mode shapes if applied to all measured frequency response functions. In addition to reducing

noise and truncation errors, the exponential window will also reduce errors often occur when testing lightly damped systems in which the damping varies with the measurement position on the structure.

Because the exponential window increases the apparent damping in the resonance modes, there is a tendency ofthe window to couple closely spaced resonance modes. Zoom transform analysis may be required in some cases to allow sufficient resolution of closely spaced modes when using the exponential window.

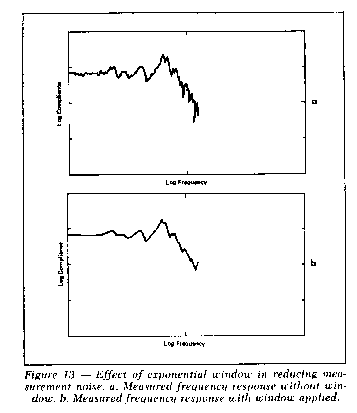
The use of the exponential window for reducing noise effects in the response signal is illustrated in Figure 13. In this case the structure is fairly heavily damped, so that the response signal decays substantially in the first part of the time­sample. It is seen that the application of the window provides a very noticeable smoothing effect on the measured frequency response function. Notice also that the window has not changed the resonance frequencies.

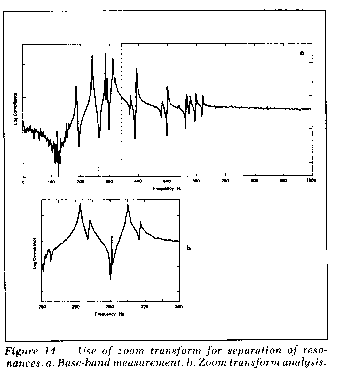
Zoom Transform. Zoom transform analysis is discussed in some detail along with several examples in Reference 2. It is a very valuable tool in impluse testing, as it is in other frequency response measurement techniques. The effect of the zoom transform is to increase the resolution of the analysis by allowing independent selection of the upper and lower frequency limits of the analysis band. With the zoom transform, for example, it is possible to perform an analysis in the frequency range from 900 to 1000 Hz as opposed to the conresponding base­band range of 0 to 1000 Hz, resulting in a 10­to­1 increase in resolution, for a given sample size N, in the 900 to 1000 Hz band. Because of the greatly increased resolution possible with the zoom transform, it can he effectively used in frequency response testing to separate closely spaced resonance modes. This is illustrated in Figure 14, which shows a base­band frequency response measurment from 0 to 1000 Hz and a zoom transform analysis of the frequency response in the range from 260 to 340 Hz.

There are two important effects of the zoom transform in

the impulse technique, both associated with the resulting increase in sample time. The first effect is to make possible much better estimates of damping in lightly damped systems. This is due to the reduction of truncation errors in the sampled response signal. The second effect, mentioned previously, is aggravation of the noise problem in both the input and response signals. The second effect makes it essential that force and response windows be applied to the data in most cases when using the zoom transform with the impulse technique.

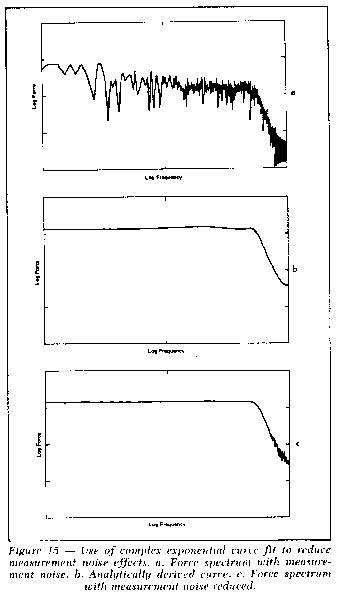
Curve Fitting. Cases of extreme measurement noise require special signal processing techniques beyond the application of sample windows. One technique that has been found to be very useful in practice is to analytically curve fit the data. Figure 15 illustrates the application of a complex exponential algorithm to a force signal with a signal­ to-noise ratio of 1. (The complex exponential algorithm is discussed in some detail in Reference 4.) Figure 15a shows the spectrum of the measured force signal and Figure 15b shows the analytically derived spectrum fitted to the data with five degrees of freedom. The quality of the fit is seen in comparing the analytical curve with the spectrum of the force signal with the measurement noise reduced, shown in Figure 15c.

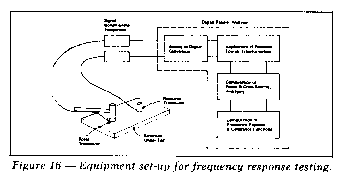
Equipment Requirements

The measurement set up for the impulse technique is shown schematically in Figure 16. The force is applied to the structure by an impactor through a load cell and the response is measured by a suitable response transducer. After passing the force and response signals through signal conditioning equipment, including appropriate amplifiers and anti­alias filters, the signals are digitized. The digitized signals are then Fourier transformed, the appropriate sample windows are applied, and the cross­spectrum and the two power spectra are computed and averaged. Finally, the frequency response and coherence functions are computed from the averaged power and cross­spectra.

The particular characteristics of each element of the test set up are described below. In addition to their individual characteristics, it is especially important that all elements be linear and have low noise when used in the impulse technique.

Impactors. The characteristics of the impactor determine the magnitude and duration of the force pulse which, in turn, determine the magnitude and content of the pulse in the frequency domain. The two impactor characteristics of most importance are its weight and tip hardness. The frequency content of the force is inversely proportional to the weight of the impactor and directly proportional to the hardness of the tip. Since the weight also determines the magnitude of the force pulse, the impactor is usually chosen for its weight and then the tip hardness is varied to achieve the desired pulse time duration. The weight of impactors commonly used in practice varies from fractions of an ounce, for ball bearings used for very high frequency testing of small structural elements such as turbine blades, to hundreds of pounds for impactors used in testing large structures. In any given measurement situation there is a limit to the weight of the impactor beyond which multiple impacts cannot be avoided. This limit is a function of the inertia of the impactor and the response of the structure.

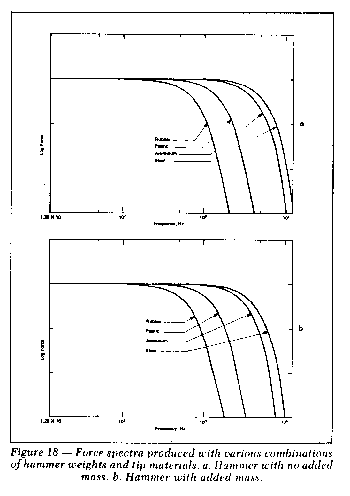
In most cases the impactor is in the shape of a hammer and the impacting is done by hand. Figure 17 shows a collection of impact hammers and tips that are applicable to a wide range of structures. Figures 18a and 18b show the

frequency spectra of the force impulse produced with a hammer with different tips and with mass added to the hammer.

The magnitude and time duration of the force pulse depend on the dynamic characteristics of the structure at the impact location as well as the hammer characteristics. For example it may be impossible to excite a weak structure such as thin sheetmetal with a sufficiently short duration impulse and still maintain the desired force magnitude using an impactor. The manner in which the impactor is applied to the structure also affects the magnitude and width of the pulse. It is important that there be moderate consistency in the impact from one sample to the next to insure that the proper frequency content of the force pulse is maintained and that the maximum signal­to­noise ratio is achieved without instrumentation overload.

Measurement Transducers. At least two transducers are required to obtain calibrated frequency response measurements: a force transducer and a response transducer. Triaxial measurements, of course, require three response transducers. The force transducer may either be part of the impactor or be mounted directly onto the structure under test. If the force transducer is mounted on the structure, then its mass­loading effects on the structure must be accounted for. If it is mounted on the impactor, then it is necessary to calibrate the impactor/transducer combination because the actual sensitivity of the transducer on the impactor can vary from its independent sensitivity by as much as 30% due to the impactor tip characteristics. Calibration of impactors is discussed in detail in the Appendix. The response transducers used in impact testing are usually accelerometers, but any suitable response transducer may be used. Displacement probes and microphones are sometimes used when transducer contact with the structure is undersirable.

Signal Conditioning Equipment. The signal condition equipment consists of the appropriate transducer amplifiers and the low­pass filters required to prevent aliasing errors. Linearity of this equipment is important because of the nature of the force and response signals, but the two characteristics of special importance in impact testing are their signal­to­noise ratios and their response to overloads. The importance of low measurement noise has already been discussed. The response to overloads is important because it is desirable to have the amplitude of the force and response signals as high as possible relative to the input range of the equipment in order to minimize noise, and variations in the impacting can frequently cause overloading. It is essential, therefore, that overloads be recognizable in the output signals. Some charge amplifiers have multiple amplifier stages with characteristics such that if the input stage is overloaded the succeeding stages give the signal a nearly normal, unclipped appearance, making it very difficult to detect overloads. This can lead to very poor estimates of frequency response.

Anti­alias filters can also disguise overloads. For this reason it is good practice to by­pass the filters and examine the signals for overloads with the analyzer set on its maximum frequency range when preparing for a test.

Analysis System. The analyzer consists of analog­to­digital converters and a system for performing a discrete finite Fourier transformation and the subsequent averaging and data manipulation required to compute the frequency response and coherence functions. The dynamic range of the analog­to­digital converters is determined by the number of bits in the digital code used in the conversion process. Most converters in common use have sufficient dynamic range for the impulse technique, but it is important that the input range of the converter be properly set for the force and response signals in order to keep the digitizer noise to a minimum.

There are several types of analysis systems being used today for frequency response testing. One type of system utilizes time sharing access to a large central computer to perform part or all of the Fourier transformation and data manipulation tasks. Other types of analyzers perform all Fourier transformation and data manipulation on site, either in a hard­wired system or a dedicated minicomputer. Any of these various types of systems can be used in the impulse technique The speed and accuracy of the analysis depends on the particular characteristics of'the system. For general use in impact testing it is very desirable that the system have zoom transform capability and be able to apply the appropriate sample windows to the data. It is also desirable that the analyzer have analytical curve fitting capability in order to handle data with high measurement noise and assist in extracting modal parameters from measured data

Measurement Procedures

Equipment Calibration and Set Up. The first step is to assemble the proper signal conditioning and analysis equipment as discussed above. Next, the impactor and the force and response transducers are selected. Then, with the anti­alias filters by­passed and the analyzer set at a high enough frequency range to avoid aliasing errors, the mass and tip hardness of the impactor are varied to give the desired magnitude and duration of the force pulse at all test locations on the structure. The impactor is then calibrated using procedures outlined in a subsequent section. Next, the input ranges of all signal conditioning and analysis equipment are set to achieve the maximum signal­to­noise ratio without overloading.

Frequency Response Testing. The first step in the testing program is to make frequency response measurments at a number of locations on the structure so that the important resonances can be identified. It may be desirable to make estimates of modal damping values at this time in addition to determining the important resonance frequencies. Analytical curve fitting routines are sometimes helpful for these tasks.

The next step is to determine the location or locations to be used for the stationary transducer during the mode

shape analyses. locations can be determined from the initial frequency response measurements. In impact testing, the response transducer is usually the stationary one and the impact is applied at suitable locations on the structure to define the resonance mode shapes.

It is good practice to monitor the force signal throughout the test program to reject poor measurements. One problem to look for, of course, is signal overload. Another cause for rejection is multiple impacts within a data sample. Multiple impacts sometimes occur, for example, when testing when lightly damped structures that bounce back against the impactor before it can be drawn away after the initial impact. Multiple impacts should be avoided because the resulting frequency spectrum will have zeros due to the periodic nature of the signal. In other words, very low levels of force will occur at certain frequencies, with resulting poor signal­to­noise ratio at those frequencies. Further errors are introduced when sample windows are applied to multiple impact data because the windows as­ a single­impulse form.

The coherence function is also helpful in monitoring the quality of the frequency response measurements. It was pointed out previously that the number of averages used in the impulse technique was not sufficient in most cases to significantly reduce the cross­spectrum bias error. However, noncoherent noise in the measured signals will increase the variance of the coherence function, giving it a "noisy" appearance. 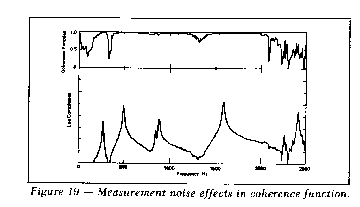This effect is illustrated in Figure 19, where the noise effects are apparent in the coherence funcin the vicinity of the anti­resonance frequencies. This is due to the low level of the response signal at the anti-resonances and the correspondingly reduced signal­to­noise ratio.

For each frequency response measurement the appropriate signal processing techniques are used to reduce the effects of noise and to achieve the desired frequency resolution. For mode shape analysis some type of curve fitting may be required in some cases to extract the modal coefficients. Common practice with the impulse technique, however, is to use the quadrature (imaginary) component of the frequency response to compute the mode shapes. as this gives satisfactory results in most cases.

Examples

Example No. 1. This example compares the results of frequency response measurements made with the impulse technique and the more traditional swept­sine technique. The measurements were made on a milling machine to determine the frequency response between the workpiece and the cutting tool. For the impact tests the force was applied to the workpiece and the relative response between the workpiece and the cutting tool was measured. The analysis was performed using a digital Fourier analyzer. For the swept­sine tests a hydraulic exciter was used to apply a force between the tool and the workpiece and the absolute motion of the workpiece was measured. 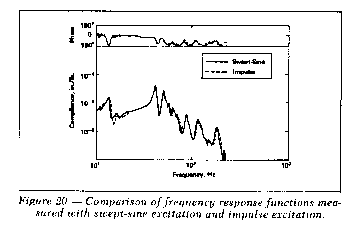This analysis was performed on an analog transfer function analyzer. The resulting frequency response measurements are shown in Figure 20, and it is seen that there is very good agreement between the results produced with the two methods.

The frequency response measurement using the impulse technique was based on only one impact, and the impact and analysis took only about two seconds to complete. This compares to a minimum often minutes required to perform the swept­sine analysis. Additional time savings were realized in the test set up. For the impact test no fixturing or elaborate exciter system was required. It was, however, necessary to insure that all backlash had been taken up in the milling machine. This was achieved by impacting the machine several times before making the measurement impact.

Example No. 2. The impulse technique can often be used to measure the frequency response of an operating system. This is usually not possible with other techniques because of the transducer and exciter fixturing that must be attached to the structure. This example discusses the application of the impulse technique to the frequency response analysis of a grinder.

An aluminum disc was manufactured and installed to

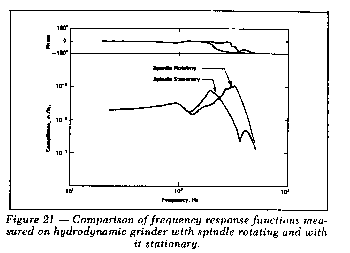
simulate the grinding wheel. The problem of applying a purely radial impact to the rotating wheel was solved by suspending a light teflon flap such that it rode on the periphery of the aluminum disc. When the disc was impacted, the radial impulse was transferred to the disc while the teflon flap prevented any tangential component from being transmitted to the rotating disc. A displacement probe was mounted on the non­rotating workpiece to measure the relative motion between the grinding wheel and the workpiece. The frequency response was measured for the grinder both with the spindle rotating and with it stationary. The resulting frequency response measurements are shown in Figure 21. This figure clearly shows the effect of the hydrodynamic spindle on the system response.

Summary

The impulse technique is generally the fastest and easiest method of exciting a structure for frequency response testing. In some cases it is the only practical method of exciting a structure. However, the particular characteristics of the resulting force and response signals often lead to serious noise and signal truncation problems that require special signal processing techniques to overcome. Also, the impulse technique is ill­suited for frequency response testing of highly nonlinear structures and certain other types of structures.

The major use of the impulse technique is in problems where moderately accurate estimates of modal parameters and mode shapes will suffice. This includes a wide range of structural dynamics problems involving fatigue failures, vibration, and noise. It generally does not produce results of sufficient accuracy for use in developing system simulation models.

As people involved in structural frequency response testing develop confidence in applying the impulse technique, it is expected to become the most widely used excitation technique.

References

1. Ramsey, K.A., "Effective Measurements for Structural Dynamics Testing - Part I," Sound and Vibration, Vol 9, No. 11, 1975

2. Ramsey, K.A., "Effective Measurements for Structural Dynamics Testing - Part II," Sound and Vibration, Vol 10, No. 4, 1976

3. Halvorsen, W.G., and Bendat, J.S., "Noise Source Identification Using Coherent Output Power Spectra," Sound and Vibration, Vol. 9, No. 8, 1975