Digital Fourier analyzers have opened a new era in structural dynamics testing. The ability of these systems to measure a set of structural transfer functions quickly and accurately and then operate on them to extract modal parameters is having a significant impact on the product design and development cycle. In order to use these powerful new tools effectively, it is necessary to have a basic understanding of the concepts which are employed. In Part I of this article, the structural dynamics model was introduced and used for presenting the basic mathematics relative to modal analysis and the representation of modal parameters in the Laplace domain. Part I concluded with a section describing the basic theoretical concepts relative to measuring transfer and coherence functions with a digital Fourier analyzer.

Part II presents an introductory discussion of several techniques for measuring structural transfer functions with a Fourier analyzer. Broadband testing techniques are stressed and digital techniques for identifying closely coupled modes via increased frequency resolution are introduced.

Certainly one of the most important areas of structural dynamics testing is the use of modern experimental techniques for modal analysis. The development of analytical and experimental methods for identifying modal parameters with digital Fourier analyzers has had a dramatic impact on product design in a number of industries. The application of these new concepts has been instrumental in helping engineers design mechanical structures which canymore payload, vibrate less, nun quieter, fail less frequently, and generally behave according to design when operated in a dynamic environment.

Making effective measurements in structural dynamics testing can be a challenging task for the engineer who is new to the area of digital signal analysis. These powerful new signal analysis systems represent a significant departure from traditional analog instrumentation in teens of theory and usage. By their very nature, digital techniques require that all measurements be discrete and of finite duration, as opposed to continuous duration in the analog domain. However, the fact that digital Fourier analyzers utilize a digital processor enables them to offer capabilities to the testing laboratory that were unheard of only a few years ago.

Modal analysis, an important part of the overall structural dynamics problem, is one area that has benefited tremnendously from the advent of digital Fourier analysis. The intent of this article is to present some of the important topics relative to understanding and making effective measurements for use in modal analysis. The engineer using these techniques needs to have a basic understanding of the theory on which the identification of modal parameters is based, in order to make a measurement which contains the necessary information for parameter extraction.

Part I of this article introduced the structural dynamics model and how it is represented in the Laplace or s­domain. The Laplace formulation was used, because it provides a convenient model to present the definition of modal parameters and the mathematics for describing a mode of vibration.

In this part, we will diverge from the mathematics and present some practical means for measuring structural transfer functions for the purpose of modal parameter identification. Unfortunately, the scope of this article does not penmit a thorough explanation of many factors which are important to the measurement process, such as sampling, aliasing, and leakage.¹ Instead, we will concentrate more on different types of excitation and the importance of adequate frequency resolution.

Identification of Modal Parameters: a Short Review

In Part I we derived the time, frequency and Laplace or e­plane representation of a single­degree­of­freedom system, which has only one mode of vibration.

The time domain representation is a statement of Newton's second law

(1)

This equation of motion gives the correct time domain response of a vibrating system consisting of a single mass, spring and damper, when an arbitrary input force is applied.

The transfer function of the single­degree­of freedom system is derived in terms of its e­plane representation by introducing the Laplace transform. The transfer function is defined as the ratio of the Laplace transform of the output of the system to the Laplace transform of the input. The compliance transfer function was written as

(2)

Finally, the frequency domain form is found by applying the fact that the Fourier transform is merely the Laplace transform evaluated along the jw or frequency axis of the complex Laplace plane. This special case of the transfer function is called the frequency response function written as,

Thus, as shown in Figure 1, the motion of a mechanical system can be completely described as a function of time, frequency, or the Laplace variable, s. Most importantly, all are valid ways of characterizing a system and the choice is generally dictated by the type of information that is desired.

Because the behavior of mechanical structures is more easily characterized in the frequency domain, especially in terms of modes of vibration we will devote our attention to their frequency domain descriptions.

A mode of vibration (the k^th mode) is completely described by the four Laplace parameters: w_k, the natural frequency; 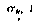, the modal damping co­efficient; and the complex residue which is expressed as two terms, magnitude and phase. The residues define the mode shapes for the system. The Fourier transfom is the tool that allows us to transform time domain signals to the frequncy domain and thus observe the Laplace domain along the frequency axis. It is possible to show that the transfer function over the entire s­plane is completely determined by its values along the jw axis, so the frequency response function contains all of the necessary information to identify modal parameters.

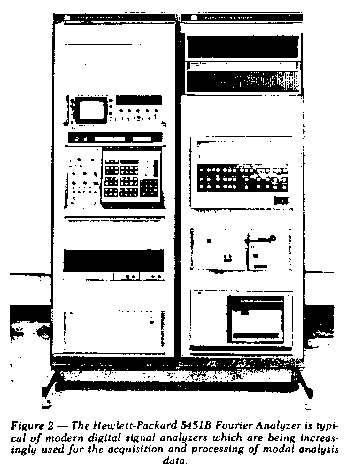
Digital Fourier analyzers, such as the one shown in Figure 2, have proven to be ideal tools for measuring structural frequency response functions (transfer functions) quickly and accurately. Coupling this with the fact that modes of vibration can be identified from measured frequency response functions by digital parameter identification techniques gives the testing laboratory an accurate and cost­effective means for quickly characterizing a structure's dynamic behavior by identifying its modes of vibration.²

The remainder of this article will attempt to introduce some of the techniques which are available for making effective frequency response measurements with digital Fourier analyzers.

Measuring Structural Frequency Response Functions

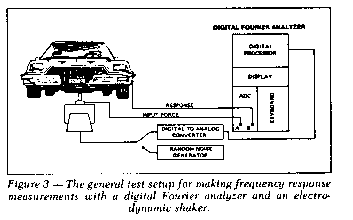
The general scheme for measuring frequency response functions with a Fourier analyzer consists of measuring simultaneously an input and response signal in the time domain, Fourier transforming the signals, and then forming the system transfer function by dividing the transformed response by the transformed input. This digital process enjoys many benefits over traditional analog techniques in terms of speed, accuracy and post­processing capability.³ One of the most important features of Fourier analyzers is their ability to form accurate transfer functions with a variety of excitation methods. This is in contrast to traditional analog techniques which utilize sinusoidal excitation. Other types of excitation can provide faster measurements

and a more accurate simulation of the type of excitation which the structure may actually experience in service. The only requirement on excitation functions with a digital Fourier analyzer is that they contain energy at the frequencies to be measured.

The following sections will discuss three popular methods for exciting a structure for the purpose of measuring transfer functions; they are, random, transient, and sinusoidal excitation. To begin with, we will restrict our discussion to baseband measurements; i.e., measurements made from dc (zero frequency) to some F_max (maximum frequency). The procedures for using these broadband stimuli (except transient) are all very similar. They are typically used to drive a shaker which, in turn, excites the mechanical structure under test. The general process is illustrated in Figure 3.

Random Excitation Techniques

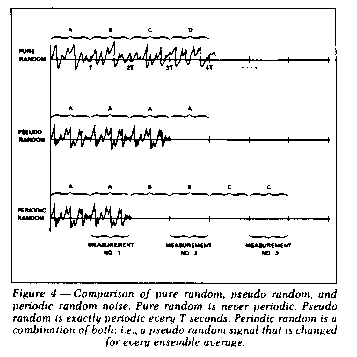
In this section, three types of broadband random excitation which can be used for making frequency response measurements are discussed. Each one possesses a distinct set of characteristics which should be understood in order to use them effectively. The three types are: (1) pure random, (2) pseudo random, and (3) periodic random.

Typically, pure random signals are generated by an external signal generator, whereas pseudo random and periodic random are generated by the analyzer's processor and output to the structure via a digital­to­analog converter, as shown in Figure 3. Figure 4 illustrates each type of random signal.

Pure Random

Pure random excitation typically has a Gaussian distribution and is characterized by the fact that it is in no way periodic, i.e., does not repeat. Typically, the output of an independent signal generator may be passed through a bandpass filter in order to concentrate energy in the band of interest. Generally, the signal spectrum will be flat except for the filter roll­off and, hence, only the overall level is easily controlled.

One disadvantage of this approach is that, although the shaker is being driven with a flat input spectrum, the structure is being excited by a force with a different spectrum due to the impedance mismatch between the structure and shaker head. This means that the force spectrum is not easily controlled and the structure may not be forced in the optimum manner. Since it is difficult to shape the spectrum because it is not generally controlled by the computer, some form of closed­loop force control system would ideally he used. Fortunately, in most cases, the problem is not important enough to warrant this effort.

A more serious drawback of pure random excitation is that the measured input and response signals are not periodic in the measurement time window of the analyzer. A key assumption of digital Fourier analysis is that the time waveforms he exactly periodic in the observation window. If this condition is not met, the corresponding frequency spectrum will contain so­called "leakage" due to the nature of the discrete Fourier transform; that is, energy from the non­periodic parts of the signal will leak" into the periodic parts of the spectrum, thus giving a less accurate result.

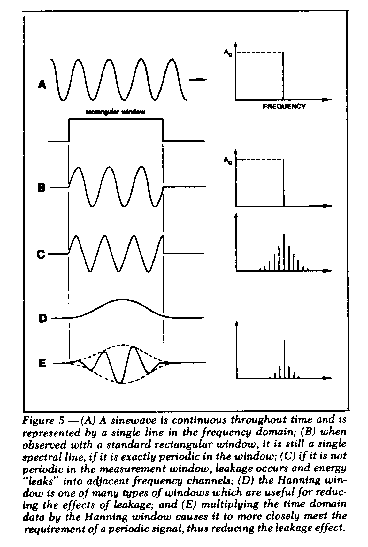
In digital signal analyzers, non­periodic time domain data is typically multiplied by a weighting function such as a Hanning window to help reduce the leakage caused by non­periodic data and a standard rectangular window.

When a non­periodic time waveform is multiplied by this window, the values of the signal in the measurement window more closely satisfy the requirements of a periodic signal. The result is that leakage in the spectrum of a signal which has been multiplied by a Hanning window is greatly reduced.

However, multiplication of two time waveforms, i.e., the non­periodic signal and the Hanning window, is equivalent to the convolution of their respective Fourier transforms (recall that multiplication in one domain is exactly equivalent to convolution in the other domain). Hence, although multiplication of a non­periodic signal by a Hanning window reduces leakage, the spectrum of the signal is still distorted due to the convolution with the Fourier transform of the Hanning window. Figure 5 illustrates these points for a simple sinewave.

With a pure random signal, each sampled record of data T seconds long is different from the preceeding and following records. (Figure 4). This gives rise to the single most important advantage of using a pure random signal for transfer function measurement. Successive records of frequency domain data can be ensemble averaged together to remove non­linear effects, noise, and distortion from the measurement. As more and more averages are taken, all of these components of a structure's motion will average toward an expected value of zero in the frequency domain data. Thus, a much better measure of the linear least squares estimate of the response of the structure can be obtained.³

This is especially important because digital parameter estimation schemes are all based on linear models and the premise that the structure behaves in a linear manner. Measurements that contain distortion will be more difficult to handle if the modal parameter identification techniques used are based upon a linear model of the structure's motion.

Pseudo­Random

In order to avoid the leakage effects of a non­periodic signal, a waveform known as pseudo random is commonly used. This type of excitation is easy to implement with a digital Fourier analyzer and its digital­to­analog (DAC) converter. The most commonly used pseudo random signal is referred to as "zero­variance random noise." It has uniform spectral density and random phase. The signal is generated in the computer and repeatedly output to the shaker through the DAC every T seconds (Figure 4). The length of the pseudo random record is thus exactly the same as the analyzer's measurement record length (T seconds), and is thus exactly periodic in the measurement window.

Because the signal generation process is controlled by the analyzer's computer, any signal which can be described digitally can be output through the DAC. The desired output signal is generated by specifying the amplitude spectrum in the frequency domain; the phase spectrum is normally random. The spectrum is then

Fourier transformed to the time domain and output through the DAC. Therefore, it is relatively easy to alter the stimulus spectrum to account for the exciter system characteristics.

In general, besides providing leakage­free measurements, a technique using pseudo random noise can often provide the fastest means for making a statistically accurate transfer function measurement when using a random stimulus. This proves to be the case when the measurement is relatively free of extraneous noise and the system behaves linearly, because the same signal is output repeatedly and large numbers of averages offer no significant advantages other than the reduction of extraneous noise.

The most serious disadvantage of this type of signal is that because it always repeats with every measurement record taken, non­linearities, distortion, and periodicities due to rattling or loose components on the structure cannot be removed from the measurement by ensemble averaging, since they are excited equally every time the pseudo random record is output.

Periodic Random

Periodic random waveforms combine the best features of pure random and pseudo random, but without the disadvantages; that is, it satisfies the conditions for a periodic signal, yet changes with time so that it excites the structure in a truly random manner.

The process begins by outputting a pseudo random signal from the DAC to the exciter. After the transient part of the excitation has died out and the structure is vibrating in its steady­state condition, a measurement is taken; i.e., input, output, and cross power spectrums are formed. Then, instead of continuing to output the same signal again, a different uncorrelated pseudo random signal is synthesized and output (refer again to Figure 4). This new signal excites the structure in a new steady­state manner and another measurement is made.

When the power spectrums of these and many other records are averaged together, non­linearities and distortion components are removed from the transfer function estimate. Thus, the ability to use a periodic random signal eliminates leakage problems and ensemble averaging is now useful for removing distortion because the structure is subjected to a different excitation before each measurement.

The only drawback to this approach is that it is not as fast as pseudo random or pure random, since the transient part of the structure's response must be allowed to die out before a new ensemble average can be made. The time required to obtain a comparable number of averages may be anywhere from 2 to 3 times as long. Still, in many practical cases where a baseband measurement is appropriate, periodic random provides the best solution, in spite of the increased measurement time.

Sinusoldal Testing

Until the advent of the Fourier analyzer, the measurement of transfer functions was accomplished almost exclusively through the use of swept­sine testing. With this method, a controlled sinusoidal force is input to the structure, and the ratio of output response to the input force versus frequency is plotted. Although sine testing was necessitated by analog instrumentation, it is certainly not limited to the analog domain. Sinusoidally measured transfer functions can be digitized and processed with the Fourier analyzer or can be measured directly, as we will explain here.

In general, swept sinusoidal excitation with analog instrumentation has several disadvantages which severely limit its effectiveness:

1) Using analog techniques, the low frequency range is often limited to several Hertz.
2) The data acquisition time can be long.
3) The dynamic range of the analog instrumentation limits the dynamic range of the transfer function measurements.
4) Accuracy is often difficult to maintain.
5) Non­linearities and distortion are not easily coped with.

However, swept­sine testing does offer some advantages over other testing forms:

1) Large amounts of energy can be input to the structure at each particular frequency.
2) The excitation force can be controlled accurately.

Being able to excite a structure with large amounts of energy provides at least two benefits. First, it results in relatively high signal­to­noise ratios which aid in determining transfer function accuracy and, secondly, it allows the study of structural non­linearities at any specific frequency, provided the sweep frequency can be manually controlled.

Sine testing can become very slow, depending upon the frequency range of interest and the sweep rate required to adequately define modal resonances. Averaging is accomplished in the time domain and is a function of the sweep rate.

A sinusoidal stimulus can be utilized in conjunction with a digital Fourier Analyzer in many different ways. However, the fastest and most popular method utilizes a type of signal referred to as a "chirp." A chirp is a logarithmically swept sinewave that is periodic in the analyzer's measurement window, T. The swept sine is generated in the computer and output through the DAC every T seconds. Figure l0G shows a chirp signal. The important advantage of this type of signal is that it is sinusoidal and has a good peak­to­rms ratio. This is an important consideration in obtaining the maximum accuracy and dynamic range from the signal conditioning electronics which comprise part of the test setup. Since the signal is periodic, leakage is not a problem. However, the chirp suffers the same disadvantage as a pseudo random stimulus; that is, its inability to average out non­linear effects and distortion.

Any number of alternate schemes for using sinusoidal excitation can be implemented on a Fourier analyzer. However, they will not be discussed here because they offer few, if any, advantages over the chirp and, in fact, generally serve to make the measurement process more tedious and lengthy.

Transient Testing

As mentioned earlier, the transfer function of a system can be determined using virtually any physically realizable input, the only criteria being that some input signal energy exists at all frequencies of interest. However, before the advent of mini­computer­based Fourier analyzers, it was not practical to determine the Fourier transform of experimentally generated input and response signals unless they were purely sinusoidal.

These digital analyzers, by virtue of the fast Fourier transform, have allowed transient testing techniques to become widely used. There are two basic types of transient tests: (1) Impact, and (2) Step Relaxation.

Impact Testing

A very fast method of performing transient tests is to use a hand­held hammer with a load cell mounted to it to impact the structure. The load cell measures the input force and an accelerometer mounted on the structure measures the response. The process of measuring a set of transfer functions by mounting a stationary response transducer (accelerometer) and moving the input force around is equivalent to attaching a mechanical exciter to the struck ture and moving the response transducer from point to point. In the former case, we are measuring a row of the transfer matrix whereas in the latter we are measuring a column.²

In general, impact testing enjoys several important advantages:

1) No elaborate fixturing is required to hold the structure under test.
2) No electro­mechanical exciters are required.
3) The method is extremely fast-often as much as 100 times as fast as an analog swept­sine test.

However, this method also has drawbacks. The most serious is that the power spectrum of the input force is not as easily controlled as it is when a mechanical shaker is used. This causes non­linearities to be excited and can result in some variablity between successive measurements. This is a direct consequence of the shape and amplitude of the input force signal.

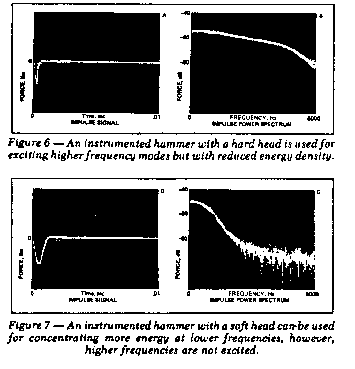
The impact force can be altered by using a softer or harder hammer head. This, in turn, alters the corresponding power spectrum. In general, the wider the width of the force impulse, the lower the frequency range of excitation. Therefore, impulse testing is a matter of trade­offs. A hammer with a hard head can be used to excite higher frequency modes, whereas a softer head can be used to concentrate more energy at lower frequencies. These two cases are illustrated in Figures 6 and 7.

Since the total energy supplied by an impulse is distributed over a broad frequency range, the actual excitation

energy density is often quite small. This presents a problem when testing heavily damped structures, because the transfer function estimate will suffer due to the poor signal­to­noise ratio of the measurement. Ensemble averaging, which can be used with this method, will greatly help the problem of poor signal­to­noise ratios.

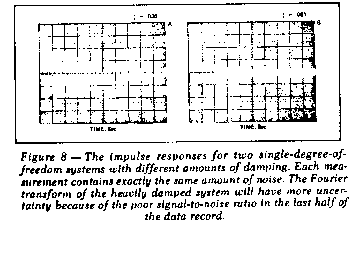
Another major problem is that of frequency resolution. Adequate frequency resolution is an absolute necessity in making good structural transfer function measurements. The fundamental nature of a transient response signal places a practical limitation on the resolution obtainable. In order to obtain good frequency resolution for quantifying very lightly damped resonances, a large number of digital data points must be used to represent the signal. This is another way of saying that the Fourier transform size must be large, since

Thus, as the response signal decays to zero, its signal­to-ratio becomes smaller and smaller. If it has decayed to a small value before a data record is completely filled, the Fourier transform will be operating mostly on noise, therefore causing uncertainties in the transfer function measurement. Obviously, the problem becomes more acute as higher frequency resolutions are needed and as more heavily damped structures are tested. Figure 8 illustrates this case for a simple single­degree­of­freedom system. In essence, frequency resolution and damping form the practical limitations for impulse testing with baseband (dc to F_max) Fourier analysis.

Since a transient signal may or may not decay to zero within the measurement window, windowing can be a serious problem in many cases, especially when the damping is light and the structure tends to vibrate for a long fume. In these instances, the standard rectangular window is unsatisfactory because of the severe leakage. Digital Fourier analyzers allow the user to employ a variety of different windows which will alleviate the problem. Typically, a Hanning window would be unsuitable because it destroys data at the first of the record-the most important part of a transient signal. The exponential window can be used to preserve the important information in the waveform while at the same time forcing the signal to become periodic. It must, however, be applied with care, especially when modes are closely spaced, for exponential smoothing can smear modes together so that they are no longer discernible as separate modes. Reference 4 explains this in more detail.

In spite of these problems, the value of impact testing for modal analysis cannot be overstressed.

It provides a quick means for troubleshooting vibration problems. For a great many structures an impact can suitably excite the structure such that excellent transfer function measurements can be made. The secret of its success rest with the user and his understanding of the physics of the situation and the basics of digital signal processing.

Step Relaxation Testing

Step relaxation is another form of transient testing which utilizes the same type of signal processing techniques as the impact test. In this method, an inextensible, lightweight cable is attached to the structure and used to pre.load the structure to some acceptable force level. The structure "relaxes" with a force step when the cable is severed, and the transient response of the structure, as well as the transient force input, are recorded.

Although this type of excitation is not nearly as convenient to use as the impulse method, it is capable of putting a great deal more energy into the structure in the low frequency range. It is also adaptable to structures which are too fragile or too heavy to be tested with the hand­held hammer described earlier. Obviously, step relaxation testing will also require a more complicated test setup than the impulse method but the actual data acquisition time is the same.

Testing a Simple Mechanical System

A single­degree­of­freedom system was tested with each type of excitation method previously discussed. Besides measuring the linear characteristics of the system with each excitation type, gross non­linearity was simulated by clipping approximately one­third of the output signal. This condition simulates a "hard stop" in an otherwise unconstrained system. The intent ot these tests was to show how certain forms of excitation can be used to measure the linear characteristics of a system with a large amount of distortion. This is extremely important to the engineer who is interested in identifying modal parameters.

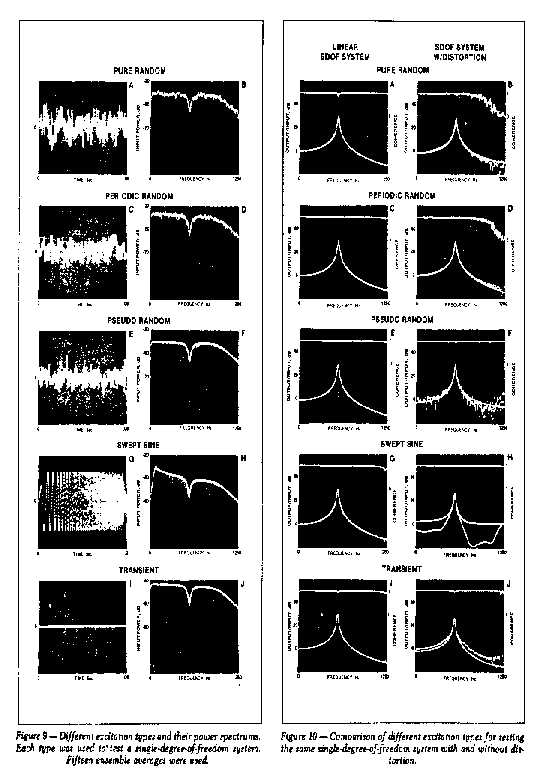
Figure 9 illustrates the form of each type of stimulus and its power spectrum after fifteen ensemble averages. Notice that the input power spectrums for both the pure random and periodic random cases have more variance than the others. This is because each ensemble average consisted of a new and uncorrelated signal for these two stimuli. The pseudo random and swept sine (chirp) signals were controlled by the analyzer's digital­to­analog converter and each ensemble average was in fact the same signal, thus resulting in zero variance. In this test, the transient signal was also controlled by the DAC to obtain record­to­record repeatability and resulting zero variance. In all cases, the notching in the power spectrums is due to the impedance mismatch between the structure and the shaker. A final interesting note is that all spectrums except the swept sine are flat out to the cut­off frequency. The roll­off of the swept sine spectrum is due to the logarithmic sweep rate. Thus, the spectrum has reduced energy density as the frequency is increased.

Recall that in Part I we discussed the use of the coherence function to assess the quality of the transfer function measurement. In Figure 10, the results obtained from testing the single­degree­of­freedom system with and without distortion are shown. In Figures 10A and 10B, the cases for pure random excitation, notice that the coherence is noticeably different from unity in the vicinity of the resonance. This is due to the non­periodicity of the signals and the

fact that Hanning windowing was used to reduce what would have otherwise been even more severe leakage. The leakage effect is much more sensitive here, due to the sharpness of the resonance, i.e., the rate of change of the function. Although the effect is certainly present throughout the rest of the band, the relatively small changes in response level between data points away from the resonance will obviously tend to minimize the leakage from adjacent channels. Although any number of different windowing functions could have been used, the phenomenon would still exist.

Figures 10C­10J show the results of testing the system with the other excitation forms. In all figures showing the distorted case, the best fit of a linear model to the measured data is also shown. The coherence is almost exactly unity for the linear cases shown in Figures l0C. E, G and I. This is because all are ideally leakage­free measurements because they are periodic in the analyzer's measurement window. For the cases with distortion, the latter three show very good coherence even though the system output was highly distorted. This apparently good value of coherence is due to the nature of the zero-variance periodic signals used as stimuli. In cases l0B and l0D, the measurements are truly random from average to average and the coherence is more indicative of the quality of the measurement. The low coherence values at the higher frequencies are primarily a result of the poor signal energy available. The conclusion is that the coherence function can be misleading if one does not understand the measurement situation.

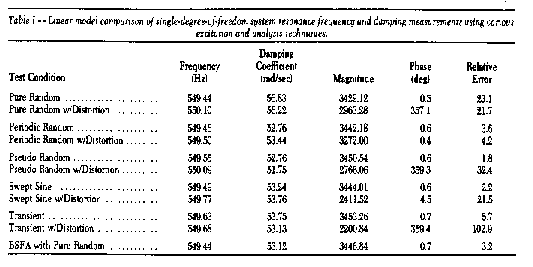
Even though the system was highly distorted, it is apparent that the pure random and periodic random stimuli provided the best means for transfer function measurements, as seen in Figures l0B and l0D. Again, this is due to their ability to effectively use ensemble averaging to remove the distortion components from the measurement. The distortion cannot be removed using the other types of periodic stimuli and this is evident in Figures l0F, H and J. The results obtained from fitting a liner model to the measured data are given in Table I.

In all cases where the linear motion was measured, each type of excitation gave excellent results, as indeed they should. The one item worthy of mention is the estimate of damping with the pure random result. In this case, the value is about 7% higher than the correct value. This error is due to the windowing effect on the data. In this test, a Hanning window was used. However, any number of other windows could have been used and error would still be present. Further evidence of the Hanning effect on the data is shown by the error between the linear model and the measured data.

Of considerable importance is the data for the simulated distortion. The primary conclusion that can be drawn from these data is that the periodic random stimulus provides a good means for measuring the linear response of a linear system and is clearly superior to a pure random stimulus. It is also the best possible excitation for measuring the linear response of a system with distortion. Evidence of this is seen in the quality of the parameter estimates in Table I and the relative error (the error index between the ideal linear model and the measured data). The principal characteristics of each type of excitation are summarized in Table II.

Increasing Frequency Resolution

Certainly the single most important factor affecting the accuracy of modal parameters is the accuracy of the transfer function measurements. And, in general, frequency resolution is the most important parameter in the measurement process. In other words, it is simply not possible to extract the correct values of the modal parameters when there is inadequate information available to process. Modern curve fitting algorithms are highly dependent on adequate resolution in order to give correct parameter estimates, including mode shapes.

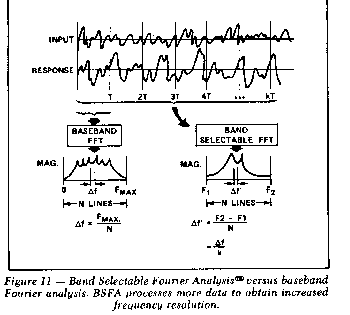
In this section we will introduce Band Selectable Fourier Analysis (BSFA), the so­called "zoom" transfonn. BSFA is a measurement technique in which the Fourier transform is performed over a frequency band whose lower and upper limits are independently selectable. This is in contrast to standard baseband Fourier analysis, which is always computed over a frequency range from zero frequency to some maximum frequency, F_max. From a practical viewpoint, in many complex structures, modal density is so great, and modal coupling (or overlap) so strong, that increased frequency resolution over that obtainable with baseband techniques is an absolute necessity for achieving reliable results.

In the past, many digital Fourier Analyzers have been limited to baseband spectral analysis; that is, the frequency band under analysis always extends from dc to some maximum frequency. With the Fourier transform, the available number of discrete frequency lines (typically 1024 or 512) are equally spaced over the analysis band. This, in turn, causes the available frequency resolution to be, 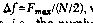, where N is the Fourier transform block size, i.e., the number of samples describing the real­time function. There are N/2 complex (magnitude and phase) samples in the frequency domain. Thus, F_max and the block size, N, determine the maximum obtainable frequency resolution.

The problem with baseband Fourier analysis is that, to increase the frequency resolution for a given value of F_max the number of lines in the spectrum (i.e., the block size) must increase. There are two important reasons why this is an inefficient way to increase the frequency resolution:

1) As the block size increases, the processing time required to perform the Fourier transform increases.
2) Because of available computer memory sizes, the block size is limited to a relatively small number of samples(typically a maximum of 4096).

More recently, however, the implementation of BSFA has made it possible to perform Fourier analysis over a frequency band whose upper and lower frequency limits are independently selectable. BSFA provides this increased frequency resolution without increasing the number of spectral lines in the computer.

BSFA operates on incoming time domain data to the analyzer's analog­to­digital converter or time domain data that has previously been recorded on a digital mass storage device. BSFA digitally filters the time domain data and stores only the filtered data in memory. The filtered data corresponds to the frequency band of interest as specified by the user. The procedure is completed by performing a complex Fourier transform on the filtered data.

Of fundamental importance is the fact that the laws of nature and digital signal processing also apply to the BSFA situation. Since the frequency resolution is always equal to the reciprocal of the observation time of the measurement, delta f = 1/T, the digital filters must process T seconds of data to obtain a frequency resolution of 1/T in the analysis band. Whereas in baseband Fourier analysis the maximum resolution is always 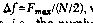the resolution with BSFA is 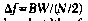where BW is the independently selectable bandwidth of the BSFA measurement. Therefore, by restricting our attention to a narrow region of interest below F_max and concentrating the entire power of the Fourier transform in this interval, an increase in frequency resolution equal to F_max/BW can be obtained (Figure 11).

The other significant advantage of BSFA is its ability to increase the dynamic range of the measurement to 90 dB or more in many cases. The increased dynamic range of BSFA is a direct result of the extremely sharp roll­off and out­of-band rejection of the pre­processing digital filters and of the increased frequency resolution which reduces the effect of the white quantizing noise of the analyzer's analog-to­digital converter.⁵ Certain types of BSFA filters can provide more than 90 dB of out­of­band rejection relative to a full scale in­band spectral line, a characteristic which is not matched by more traditional analog range translators (see Figure 12).

The simple single­degree­of­freedom system which was tested with the various excitation types was also tested with BSFA using pure random excitation We saw that in the baseband case, pure random was the least desirable signal because of the associated leakage and the resulting distortion of the transfer function waveform introduced by the Hanning window. By using BSFA, leakage is no longer an important source of error because of the great increase in the number of spectral lines used to describe the system. Figure 13 shows the coherence and transfer function between 524.6 Hz and 579.6 Hz with a resolution of 0.269 Hz, an increase of more than 18 over the baseband result. Note that the coherence is almost exactly unity, indicating the

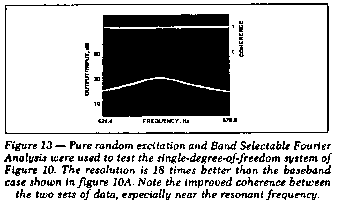
absence of any error due to leakage, and confirming the quality of the BSFA measurement. As shown in Table I, the use of BSFA eliminates the error caused by the leakage in the baseband measurement.

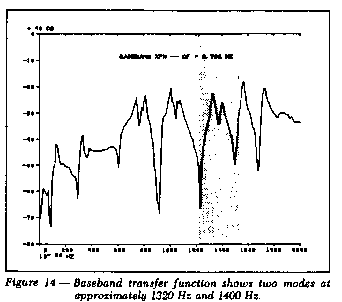
A Practical Problem. To illustrate the importance of BSFA, a mechanical structure was tested and modes in the area of 1225 Hz to 1525 Hz were to be investigated. Figure 14 is a typical baseband (dc­F_max) transfer function measurement. It was taken with the following parameters:

Pure random noise was used to excite the structure through an electro­dynamic shaker.

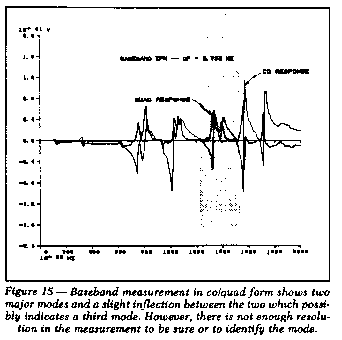
The Inadequacy of the Baseband Measurement. Note that two modes are clearly visible between 1225 Hz and 1525 Hz. This same measurement is shown in rectangular or co/quad form in Figure 15. Again, by examining the quadrature response, the two modes are seen, However, there is also a slight inflection in the response between these two modes which indicates that yet a third mode may be present. But there is insufficient frequency resolution to adequately define the mode.

Returning to Figure 15, a partial display of the region between 1225 and 1525 Hz was made. The expanded quadrature display is shown in Figure 16. Realize that this represents no increase in frequency resolution, only an expansion of the plot. Clearly, only two modes were found.

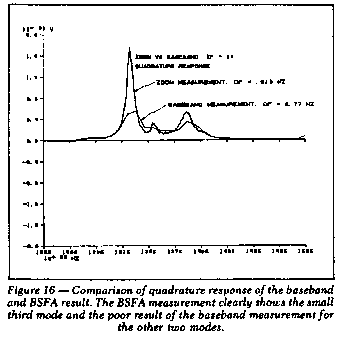
Accurate Measurements with BSFA. In order to accurately define the modes in this region, the structure was re­tested using Band Selectable Fourier Analysis (BSFA). All 512 lines of spectral resolution were placed in a band from 1225 to 1525 Hz, resulting in a resolution of 0.610 Hz instead of 9.76 Hz, as in the baseband measurement. The quadrature response attained with the BSFA is also shown in Figure 16 for comparative purposes. Note that three modes are now clearly visible. The small (third) mode of approximately 1350 Hz is now well defined, whereas it was not even apparent before. In addition, the magnitude of the first mode at 1320 Hz is seen to be at least three times greater in magnitude than the result indicated by the baseband measurement. 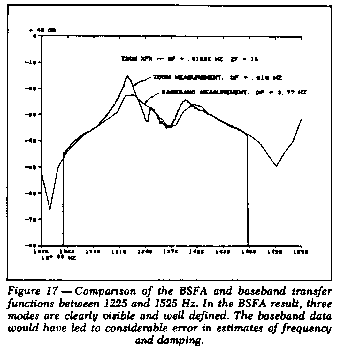The corresponding results in log form are shown in Figure 17. This BSFA result was obtained by using only a 16:1 resolution enhancement. Enhancements of more than 100:1 are possible with BSFA.

Implications of Frequency Resolution in Determining Modal Parameters and Mode Shapes. Referring again to Figure 15, we can clearly see the necessity of using adequate frequency resolution for making a particular measurement. In addition, it is important to understand how the baseband result would lead to an incorrect answer in terms of modal parameters and mode shape.

A) Modal Parameters. If the baseband result is compared to the BSFA result for the 1320 Hz mode it is obvious that the baseband result would indicate that the mode is much more highly damped than it actually is. The second small mode (1350 Hz) would not even be found, and the 1400 Hz mode would also have the wrong damping. Close inspection also shows that the estimate of the resonance frequency for the 1320 Hz mode would have significant error.

B) Mode Shape. Any technique for estimating the mode shape coefficients (e.g., quadrature response, circle fitting, differencing, least squares, etc.) would clearly be in error since it is apparent that the BSFA result shows a quadrature response at least three times greater than the baseband result.

Although the proceeding example presented a case where the use of BSFA was a necessity, it is very easy for the engineer to be misled into believing he has made a measurement of adequate resolution when in fact he has not. The following concluding example illustrates this point and presents the estimates of the modal parameters for each case.

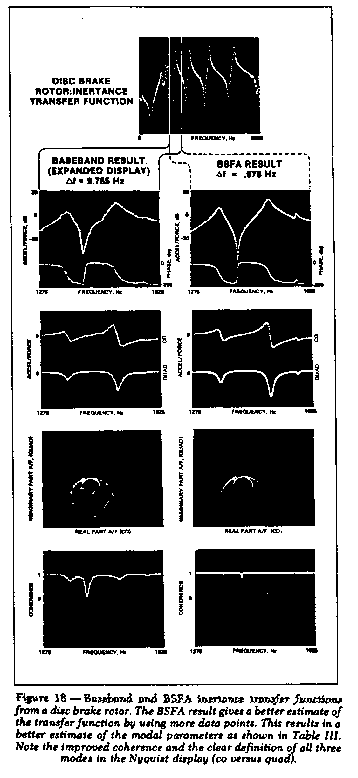
A disc brake rotor was tested using an electro­dynamic shaker and pure random noise as a stimulus. A load cell was used to measure the input force and an accelerometer mounted near the driving point was used to measure the response. The baseband measurement had a resolution of 9.76 Hz. As can be seen in Figure 18A, the two major modes at about 1360 Hz and 1500 Hz appear to be well defined. An expanded display (no increased resolution) from 1275 Hz to 1625 Hz clearly shows the two large modes and a much smaller mode at about 1580 Hz.

The rotor was re­tested using BSFA and the two sets of data are compared in Figure 18. This data clearly shows the value of BSFA. The BSFA data provides increased definition of the modal resonances, as can be seen by comparing the baseband and BSFA results. The validity of each result is reflected in the respective coherence functions. The baseband transfer function contains inaccuracies due to the Hanning effect, as well as inadequate resolution. The coherence for the BSFA measurement is unity in the vicinity of all three modal resonances, indicating the quality of the transfer function measurement. Further proof of the increased modal definition is shown in the BSFA Nyquist plot (co versus quad). Here, all three modes are clearly discernible and form almost perfect circles, indicating an excellent measurement, almost totally free of distortion. In the baseband result, only three or four data points were available in the vicinity of each resonance, whereas in the BSFA data many more points are used.

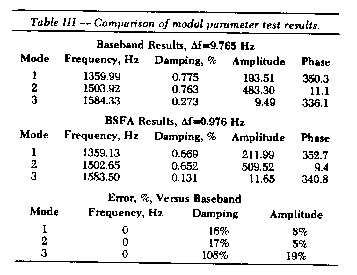
The modal parameters for all three modes were identified from the baseband and BSFA data and the results are shown in Table III. Comparison of results emphasizes the need for BSFA when accurate modal parameters are desired.

In summary, no parameter identification techniques are capable of accurately identifying modal parameters or mode shapes when the frequency resolution of the measurement is not adequate.

Summary

We have seen that frequency response functions can be used for identifying the modes of vibration of an elastic structure and that the accurate measurement of the frequency response functions is the most important factor affecting the estimates of the modal parameters.

Pure random, pseudo random, periodic random, swept

sine, and transient techniques for baseband Fourier analysis were discussed. All types of stimuli, except for pure random, gave excellent results when used for testing a linear system. The pure random result contained some error because its non­periodicity in the measurement window required that Hanning be used on the input and response waveforms, resulting in some distortion of the transfer function.

For systems with distortion, periodic random offers significant advantages over the other types of stimuli. It is best able to measure the linear response of distorted systems. This means that modal parameters extracted from transfer functions measured with periodic random will be more accurate. None of the techniques discussed are capable

of compensating for inadequate frequency resolution. Band Selectable Fourier Analysis was introduced as a means for arbitrarily increasing the frequency resolution of the frequency response measurement by more than 100 times over standard baseband measurements. BSFA's increased resolution provides the best possible means for making measurements for the identification of modal parameters and, in a great number of practical problems, is the only feasible approach.

References

1. Fourier Analyzer Training Manual, Application Note 140-0, Hewlett-Packard Company.
2. Ramsey, K. A., "Effective Measurments for Structural Dynamics Testing Part I, Sound and Vibration, November 1975."
3. Roth, Peter, "Effective Measurements Using Digital Signal Analysis," IEEE Spectrum, pp. 62-70, April 1971
4. Richardson, M., "Modal Analysis Using Digital Test Systems," Seminar on Understanding digital control and Analysis is Vibration Test Systems, Shock and Vibration Information Center publication, May 1975.
5. McKinney, W., "Band Selectable fourier Analysis," Hewlett-Packard Journal, April 1975, pp 20-24.
6. Potter, R. and Richardson, M., "Mass, Stiffness and Damping Matrices from Measured Modal Parameters," ISA Conference and Exhibit, New York City, October 1974.
7. Potter,R., "A General Theory of Modal Analysis for Linear Systems," Shock and Vibration Digest, November 1975.