This paper will discuss the effects of digital signal processing errors caused by improper analog to digital conversion settings. Four signal types will be analyzed: overload and underload on the input channel; and, overload and underload on the response channel. The errors will be shown to affect the quality and accuracy of the measured frequency response function. The errors which are present in the measurement will also be shown to exist as an inaccurate estimate of the modal residue obtained through curvefitting.

INTRODUCTION

Through advances in the field of dynamic analysis, structural analysts are able to predict the dynamic response of a structure through an experimental modal test. This gives the analyst a very powerful tool for structural modifications, providing the results of the modal test are an accurate representation of the dynamics of the structure.

The modal test can be divided into two parts:

1) Modal Data Acquisition, and
2) Modal Parameter Estimation

The first step of the modal data acquisition process requires analog voltages representing structural response to be converted to digital signals to conform to the requirements of digital computers. This conversion is one of the first places errors in modal data can occur. These errors will then be carried through the entire test and can distort the results of the test.

However, the modal practitioner can minimize the effects of the error once an error has been recognized. It is the intent of this paper to characterize four ADC errors and show the effect of the errors on the modal parameter estimation of the residue term. This will then enable the modal practitioner to recognize these ADC errors and the seriousness of each error on the estimate of the residue term.

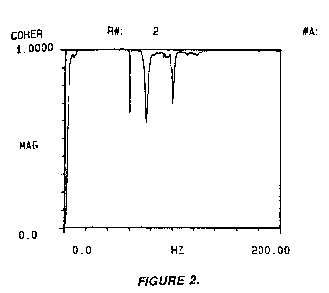
In order to speak of recognizing erroneous measurements or sets of measurements, one must first define an accurate measurement to be used for comparison. Figure 1 represents an accurate dynamic description of an engine/powertrain assembly driving point function. Figure 2 represents the coherence function for the measurement in Figure 1.

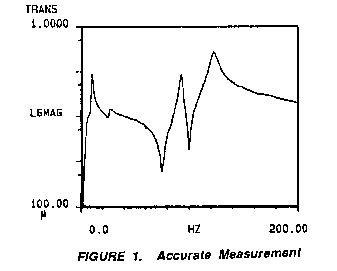
The structure was excited with burst random noise. The amplitude of the excitation was optimized to a 1 volt ADC setting on the Fourier analyzer. The optimization entailed increasing the amplitude of the signal until an ADC overflow occurred and then reducing the amplitude just enough to avoid the overflow completely.

A similar type optimization was performed on the response channel, except only by adjusting the gain of the power amplifier.

The first set of errors to be discussed will be ADC overloading. ADC overloading can be defined as providing a signal to the ADC greater than the available dynamic range of the current ADC setting. Typically, an analyzer will have up to 80 dB of dynamic range. An overload will occur if the dynamic range of the power spectrum signal is greater than 80 dB. ADC overloads can occur on either input or response channels.
An ADC overload on the input can be caused by the range of the ADC set to .1 volts while maintaining a 1 volt input signal. The frequency response function (frf) and coherence function are shown in Figures 3 and 4, respectively. Overlayed on each function is the measurement and coherence of the accurate measurement.

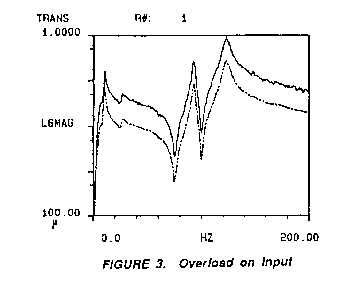
A comparison of the two frf's show substantial amplitude differences between the two functions. This bias error represents the "clipping" of the input signal. The amount of "clip" is equivalent to the maximum level of the ADC. In this case, the maximum level is .1 volts. This example has a 1 volt signal being represented as a .1 volt signal. With the frf being a ratio of the output to input, the analyst is effectively reducing the input spectrum, thus reducing the value of the denominator term of the function. This will account for the amplification of the function as seen as the bias error in Figure 3.

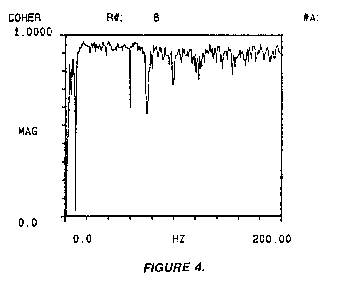
Figure 3 also shows appreciable noise imbedded in the function. This "rattiness" is caused by the Fourier transform of the "clipped" signal. This signal will cause jump discontinuities in the signal which will cause errors when the time domain signal is transformed to the frequency domain via the Fourier transform.

A similar overload condition can occur on the response channel. The response signal is maintained at 1 volt and the ADC setting is erroneously set at .1 volt. Figure 5 represents the frf measured in this condition. The amplitude of the frf is biased lower than the accurate measurement. This error is a function again of the clipped signal's effect on the calculation of the frequency response function. The "clipped" signal erroneously reduces the amplitude of the response signal which comprises the numerator term of the frf. This forces the ratio of the two signals to be lower than an accurate measurement.

The frf of Figure 5 shows substantial noise off resonance. The noise in the function is due to the truncated signal of the response channel. Similar to an input overload, the truncation of the signal force jump discontinuities in the time domain which will show up as errors in the frequency domain.

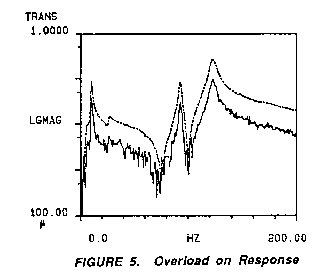
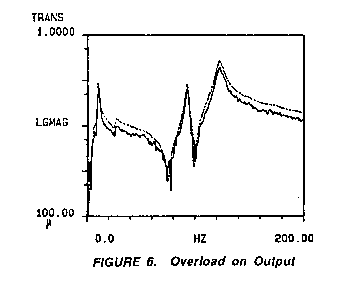
Figure 6 represents another overload on the response channel, only this time the 1 volt response signal is truncated by a .25 volt ADC setting. In comparison to Figure 5, the severity of the error can be directly correlated to the mismatch between signal strength and the ADC setting. Figure 6 shows similar characteristics to the measurement shown in Figure 5 only to a lesser degree of error from the known accurate measurement.

The second error associated with ADC settings is an underload. In an underload condition, the desired signal does not fill the entire range of the ADC's available dynamic range. The desired signal may actually reside in the noise making it undistinguishable from the noise. The severity of this condition is again dependent on the mismatch between signal strength and the ADC setting.

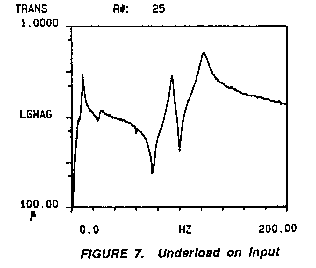
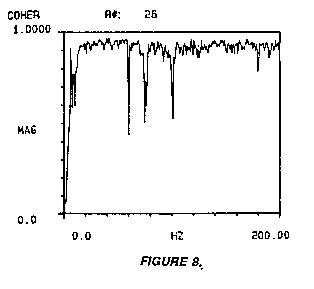
An underload condition on the input spectrum is represented in Figures 7 and 8. The measurement represents a mismatch between the signal and ADC setting by a factor of 500. The frf represented in Figure 7 is very similar to the overlayed accurate frf with the exception of the noise off resonance. However, the coherence function of Figure 8 show a degradation of the measurement throughout the spectrum. This degradation and noisiness of the frf describe the signal being lost in the noise floor of the input spectrum. The time domain representation of the signal will show digitized low level noise as the input. The ratio of the input to output signals does not show direct causality as evidenced in the coherence function.

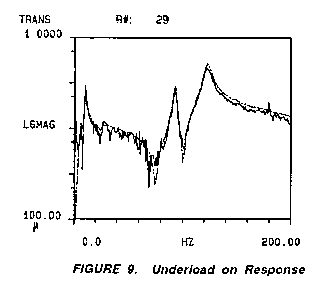
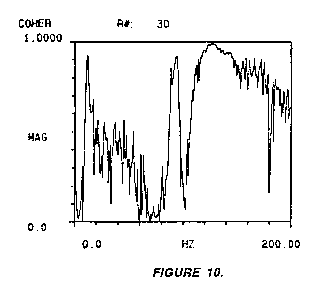
The final error to be discussed is an underload condition on the response channel. Figures 9 and 10 will show the frf and coherence function of this condition, respectively. The measured frf was acquired with the mismatch between the actual signal and the ADC setting being a factor of 400. Analysis of the data shows a noisy frf with poor coherence. The response signal is in the noise and the frf ratios the noise as a numerator term which produces noise off resonance and low coherence due to the effects of the measured response (noise) not being caused by the input signal.


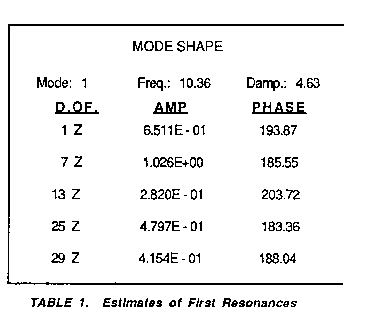
The effects of ADC errors have been seen and discussed with respect to frequency response functions. However, it is important also to realize the effects of the errors on the estimates of the modal parameters. The measured frequency response functions contain three resonances. These resonances occur at 10.36 Hz, 92.99 Hz and 122.50 Hz. A single degree of freedom polynomial was used to estimate the modal parameters for each resonance. Table 1 shows the estimates for the first resonance. DOF 1 Z corresponds to an accurate measurement with the estimate of the residue amplitude = .6511 G/lb­sec. DOF 7 Z represents the estimate for an overload on the input. The residue amplitude estimate is 1.026 G/lb­sec. This represents a 57% amplitude error. DOF 13 Z represents the overload on the response condition and is in error by 57%. DOF 25 Z represents the estimate for the underload on the input condition. The amplitude estimate is in error by 26%. The underload on the response condition corresponds to DOF 29 Z and is in error by 36%.


Similar type curvefits were run on the second and third resonance. These results are seen in Tables 2 and 3, respectively.



CONCLUSION

The ADC settings can have a very large effect on the quality of a measurement. These errors are not always easily detected if only the frequency response function is examined. The purpose of this paper is to reemphasize the importance of optimizing the ADC and amplifier settings for the best signal to noise ratios. The errors caused by ADC mismatch to signal strength are carried through to the parameter estimation process and can be seen in the estimates of the amplitude of the residue term. The amount of error present is directly proportional to the degree of mismatch between the ADC setting and signal strength. The overload errors have a more detrimental effect on the measurement than the underload conditions. By recognizing each of these error types, the analyst can better arm himself to make accurate measurements.

1. Oppenheim, A. and R. Schafer, "Digital Signal Processing", Prentice Hall, Englewood Cliffs, NJ, 585 pp.

2. Allemang, Zimmerman, Brown, "Techniques for Reducing Noise in Frequency Response Measurements", ASME Winter Annual Meeting, 12/16/79.

3. Wada, B.K., "Modal Test ­ Measurement and Analysis Requirements".

4. Ramsey, K., "Effective Measurements for Structural Dynamic Testing", Sound and Vibration, Nov. 1975.

5. Ramsey, K., "Effective Measurements for Structural Dynamic Testing, Part 2", Sound and Vibration, April 1976.