|
|
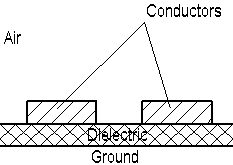
Elec2:双極コンダクタ伝送路 問題のタイプ静電場平面問題 幾何学形状
この問題の領域は底部をグランドとし、その他の3つの側面と上部は無限延と仮定します。
条件
空気の相対誘電率 e = 1 問題
コンダクタの自己/相互キャパシタンスを推定してください。
解析
外部境界の影響を回避し、領域作用をの影響を小さくするために十分に大きな長方形を定義します。一方のコンダクタを
U = 1 V とし、他方を U = 0 として、キャパシタンス・マトリックスを計算します。
自己キャパシスタンス: C11 = C22 =
Q1 / U1 相互キャパシスタンス: C12 = C21 =
Q2 / U1
ここで、電荷量 Q1 と
Q2
は、コンダクタ1と2のまわりの長方形のコンター上で評価されます。C11 と
C12 を計算するために、-6 」 x 」 0, 結果の比較
参照文献A. Khebir, A. B. Kouki, and R. Mittra, "An Absorbing Boundary Condition for Quasi-TEM Analysis of Microwave Transmission Lines via the Finite Element Method", Journal of Electromagnetic Waves and Applications, 1990. | |||||||||
●掲載例題については細心の注意を払っていますが、予告なしに内容の見直しおよび変更をさせていただくことがあります。本サイトを閲覧、ダウンロード、リンク、転載、その他の行為は著作権者の規程に同意したものとします。これによって生じる利用者各位のいかなる障害についても、責任を負うものではないこととします。あらかじめ、ご了承ください。 | |||||||||