|
|
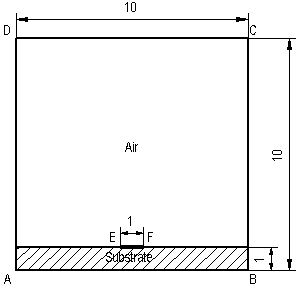
Elec1:マイクロストリップ伝送路 シールドされたマイクロストリップ伝送路は、マイクロストリップとシールドで構成されます。 問題のタイプ 静電場平面問題 幾何学形状 伝送路は、z-軸に沿って定義され、その断面図を示します。長方形ABCDはシールド断面です。ラインEFはコンダクタの一片を表わします。
条件 空気の相対誘電率 e = 1 問題 伝送路のキャパシタンスを推定してください。 解析 伝送路のキャパシタンスを計算するためのいくつかアプローチは次のとおりです。 シールドとストリップにいくつかの別個の電位を適用し、ストリップに対する発電容量を計算する。 シールドにゼロ電位を適用し、ストリップに一定の未知電位と発電容量を定義し、そのストリップに生じる電位を測定する。これらの両方のアプローチは、キャパシタンスを計算するために次式を使用します。 C = q / U. その他のアプローチとしては、電場の保持エネルギーの計算に基づきます。電圧が既知である場合には、 C = 2·W / U 2 ここで、発電容量は次式で表されます。 C = q 2 / 2·W この例題では、エネルギーに基づいたアプローチが計算精度が低いことを示します。発電容量と電圧に基づいたアプローチより精度は低いと考えられます。第1のアプローチは、あるコンターの積分値の発電容量を求めるのに必要でり、第2のアプローチは、ローカルな電位値のみを使用するため、最も単純であり、一般的に高い精度が得られます。 ExamplesフォルダーのElec1_1.pbmとElec1_2.pbmのそれぞれの問題を参照してください。その1と3が近似し、また、2と4が近似していることを確認してください 。 結果
| ||||||||||
●掲載例題については細心の注意を払っていますが、予告なしに内容の見直しおよび変更をさせていただくことがあります。本サイトを閲覧、ダウンロード、リンク、転載、その他の行為は著作権者の規程に同意したものとします。これによって生じる利用者各位のいかなる障害についても、責任を負うものではないこととします。あらかじめ、ご了承ください。 | ||||||||||