|
|
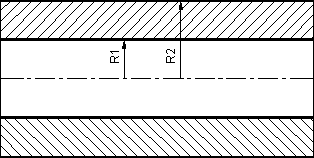
Coupl2:シリンダ構造物の温度と圧力 非常に長く、厚いシリンダの内部表面と外部表面の内部圧力と Ti ~ To の定常温度分布に関するシリンダ内の応力分布を計算してください。 問題のタイプ 熱と構造解析の線対称連成問題 幾何学形状
条件 半径 R1 = 1 cm, R2 =
2 cm 問題 応力分布を計算してください。 解析 z-軸に関するすべての物理量は変わらないため、薄いシリンダとしてモデル化することができます。モデルの軸長は任意ですが、ここでは0.2cmとします。また、シリンダの無限長と仮定できるため、軸方向の長さはゼロとします。 結果の比較 r = 1.2875cm の放射状周辺の応力は、
参照文献 S. P. Timoshenko and Goodier, "Theory of Elasticity", McGraw-Hill Book Co., N.Y., 1961, pp. 448-449. この熱と応力解析に関する問題については、ExamplesフォルダーのCoupl2HT.pbmとCoupl2SA.pbm のそれぞれの問題を参照してください。 | |||||||||
|
●掲載例題については細心の注意を払っていますが、予告なしに内容の見直しおよび変更をさせていただくことがあります。本サイトを閲覧、ダウンロード、リンク、転載、その他の行為は著作権者の規程に同意したものとします。これによって生じる利用者各位のいかなる障害についても、責任を負うものではないこととします。あらかじめ、ご了承ください。 | |||||||||